Result
Loading an infinite plate with a circular hole of radius a with stress σ, the resulting stress field is (the angle is with respect to the direction of application of the stress):
The Kirsch equations describe the elastic stresses around a hole in an infinite plate under one directional tension. They are named after Ernst Gustav Kirsch.
Loading an infinite plate with a circular hole of radius a with stress σ, the resulting stress field is (the angle is with respect to the direction of application of the stress):
In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. It treats a gas as composed of numerous particles, too small to see with a microscope, which are constantly in random motion. Their collisions with each other and with the walls of their container are used to explain physical properties of the gas—for example, the relationship between its temperature, pressure, and volume. The particles are now known to be the atoms or molecules of the gas.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed due to prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics.
The Kerr–Newman metric is the most general asymptotically flat and stationary solution of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged and rotating mass. It generalizes the Kerr metric by taking into account the field energy of an electromagnetic field, in addition to describing rotation. It is one of a large number of various different electrovacuum solutions; that is, it is a solution to the Einstein–Maxwell equations that account for the field energy of an electromagnetic field. Such solutions do not include any electric charges other than that associated with the gravitational field, and are thus termed vacuum solutions.

The Stokes parameters are a set of values that describe the polarization state of electromagnetic radiation. They were defined by George Gabriel Stokes in 1852, as a mathematically convenient alternative to the more common description of incoherent or partially polarized radiation in terms of its total intensity (I), (fractional) degree of polarization (p), and the shape parameters of the polarization ellipse. The effect of an optical system on the polarization of light can be determined by constructing the Stokes vector for the input light and applying Mueller calculus, to obtain the Stokes vector of the light leaving the system. They can be determined from directly observable phenomena. The original Stokes paper was discovered independently by Francis Perrin in 1942 and by Subrahamanyan Chandrasekhar in 1947, who named it as the Stokes parameters.
In the mathematical description of general relativity, the Boyer–Lindquist coordinates are a generalization of the coordinates used for the metric of a Schwarzschild black hole that can be used to express the metric of a Kerr black hole.
The method of image charges is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem.
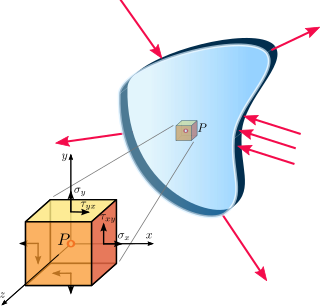
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.
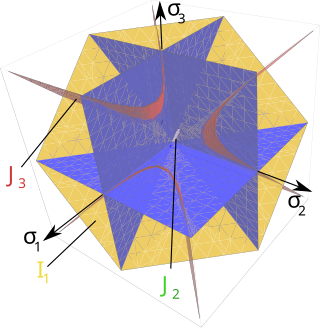
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.

In mathematics, a Scherk surface is an example of a minimal surface. Scherk described two complete embedded minimal surfaces in 1834; his first surface is a doubly periodic surface, his second surface is singly periodic. They were the third non-trivial examples of minimal surfaces. The two surfaces are conjugates of each other.
The Scherrer equation, in X-ray diffraction and crystallography, is a formula that relates the size of sub-micrometre crystallites in a solid to the broadening of a peak in a diffraction pattern. It is often referred to, incorrectly, as a formula for particle size measurement or analysis. It is named after Paul Scherrer. It is used in the determination of size of crystals in the form of powder.

The Flamant solution provides expressions for the stresses and displacements in a linear elastic wedge loaded by point forces at its sharp end. This solution was developed by A. Flamant in 1892 by modifying the three-dimensional solution of Boussinesq.

Lode coordinates or Haigh–Westergaard coordinates. are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity. Other examples of sets of tensor invariants are the set of principal stresses or the set of kinematic invariants . The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector .
In fluid dynamics, Taylor scraping flow is a type of two-dimensional corner flow occurring when one of the wall is sliding over the other with constant velocity, named after G. I. Taylor.
The fracture of soft materials involves large deformations and crack blunting before propagation of the crack can occur. Consequently, the stress field close to the crack tip is significantly different from the traditional formulation encountered in the Linear elastic fracture mechanics. Therefore, fracture analysis for these applications requires a special attention. The Linear Elastic Fracture Mechanics (LEFM) and K-field are based on the assumption of infinitesimal deformation, and as a result are not suitable to describe the fracture of soft materials. However, LEFM general approach can be applied to understand the basics of fracture on soft materials. The solution for the deformation and crack stress field in soft materials considers large deformation and is derived from the finite strain elastostatics framework and hyperelastic material models.
Chandrasekhar–Page equations describe the wave function of the spin-1/2 massive particles, that resulted by seeking a separable solution to the Dirac equation in Kerr metric or Kerr–Newman metric. In 1976, Subrahmanyan Chandrasekhar showed that a separable solution can be obtained from the Dirac equation in Kerr metric. Later, Don Page extended this work to Kerr–Newman metric, that is applicable to charged black holes. In his paper, Page notices that N. Toop also derived his results independently, as informed to him by Chandrasekhar.
Stress distribution in soil is a function of the type of soil, the relative rigidity of the soil and the footing, and the depth of foundation at level of contact between footing and soil.The estimation of vertical stresses at any point in a soil mass due to external loading is essential to the prediction of settlements of buildings, bridges and pressure.
In directional statistics, the projected normal distribution is a probability distribution over directions that describes the radial projection of a random variable with n-variate normal distribution over the unit (n-1)-sphere.