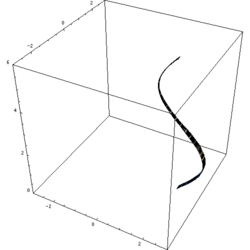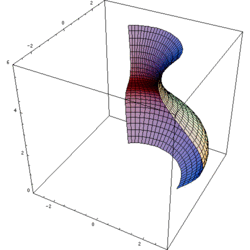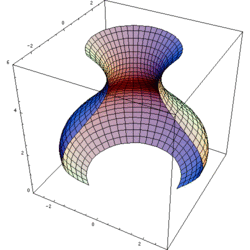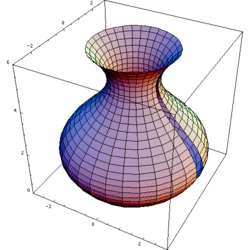
In 3D computer graphics, a lathe tool, object or function can be used to create a 3D model. [1] This is a model whose vertex geometry is produced by rotating the points of a spline or other point set around a fixed axis. The lathing may be partial; the amount of rotation is not necessarily a full 360 degrees. The point set providing the initial source data can be thought of as a cross section through the object along a plane containing its axis of radial symmetry.
The reason the lathe has this name is because it creates symmetrical objects around a rotational axis, just like a real lathe would.
Lathes are very similar to surfaces of revolution. However, lathes are constructed by rotating a curve defined by a set of points instead of a function. Note that this means that lathes can be constructed by rotating closed curves or curves that double back on themselves (such as the aforementioned torus), whereas a surface of revolution could not because such curves cannot be described by functions.