See also
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(June 2012) |
Within statistics, Local independence is the underlying assumption of latent variable models (such as factor analysis and item response theory models). The observed items are conditionally independent of each other given an individual score on the latent variable(s). This means that the latent variable(s) in a model fully explain why the observed items are related to one another. This can be explained by the following example.
Local independence can be explained by an example of Lazarsfeld and Henry (1968). Suppose that a sample of 1000 people was asked whether they read journals A and B. Their responses were as follows:
| Read A | Did not read A | Total | |
| Read B | 260 | 140 | 400 |
| Did not read B | 240 | 360 | 600 |
| Total | 500 | 500 | 1000 |
One can easily see that the two variables (reading A and reading B) are strongly related, and thus dependent on each other. Readers of A tend to read B more often (52%=260/500) than non-readers of A (28%=140/500). If reading A and B were independent, then the formula P(A&B) = P(A)×P(B) would hold. But 260/1000 isn't 400/1000 × 500/1000. Thus, reading A and B are statistically dependent on each other.
If the analysis is extended to also look at the education level of these people, the following tables are found.
|
|
Again, if reading A and B were independent, then P(A&B) = P(A)×P(B) would hold separately for each education level. And, in fact, 240/500 = 300/500×400/500 and 20/500 = 100/500×100/500. Thus if a separation is made between people with high and low education backgrounds, there is no dependence between readership of the two journals. That is, reading A and B are independent once educational level is taken into consideration. The educational level 'explains' the difference in reading of A and B. If educational level is never actually observed or known, it may still appear as a latent variable in the model.
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations .(June 2012) |
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., multivariate random variables. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied.
Psychological statistics is application of formulas, theorems, numbers and laws to psychology. Statistical methods for psychology include development and application statistical theory and methods for modeling psychological data. These methods include psychometrics, factor analysis, experimental designs, and Bayesian statistics. The article also discusses journals in the same field.
A hidden Markov model (HMM) is a Markov model in which the observations are dependent on a latent Markov process. An HMM requires that there be an observable process whose outcomes depend on the outcomes of in a known way. Since cannot be observed directly, the goal is to learn about state of by observing . By definition of being a Markov model, an HMM has an additional requirement that the outcome of at time must be "influenced" exclusively by the outcome of at and that the outcomes of and at must be conditionally independent of at given at time . Estimation of the parameters in an HMM can be performed using maximum likelihood estimation. For linear chain HMMs, the Baum–Welch algorithm can be used to estimate parameters.
A Bayesian network is a probabilistic graphical model that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). While it is one of several forms of causal notation, causal networks are special cases of Bayesian networks. Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus "error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models.

Social research is research conducted by social scientists following a systematic plan. Social research methodologies can be classified as quantitative and qualitative.
Analysis of covariance (ANCOVA) is a general linear model that blends ANOVA and regression. ANCOVA evaluates whether the means of a dependent variable (DV) are equal across levels of one or more categorical independent variables (IV) and across one or more continuous variables. For example, the categorical variable(s) might describe treatment and the continuous variable(s) might be covariates (CV)'s, typically nuisance variables; or vice versa. Mathematically, ANCOVA decomposes the variance in the DV into variance explained by the CV(s), variance explained by the categorical IV, and residual variance. Intuitively, ANCOVA can be thought of as 'adjusting' the DV by the group means of the CV(s).
In psychometrics, item response theory (IRT) is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is a theory of testing based on the relationship between individuals' performances on a test item and the test takers' levels of performance on an overall measure of the ability that item was designed to measure. Several different statistical models are used to represent both item and test taker characteristics. Unlike simpler alternatives for creating scales and evaluating questionnaire responses, it does not assume that each item is equally difficult. This distinguishes IRT from, for instance, Likert scaling, in which "All items are assumed to be replications of each other or in other words items are considered to be parallel instruments". By contrast, item response theory treats the difficulty of each item as information to be incorporated in scaling items.

A variable is considered dependent if it depends on an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule, on the values of other variables. Independent variables, in turn, are not seen as depending on any other variable in the scope of the experiment in question. In this sense, some common independent variables are time, space, density, mass, fluid flow rate, and previous values of some observed value of interest to predict future values.
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for sampling from a specified multivariate probability distribution when direct sampling from the joint distribution is difficult, but sampling from the conditional distribution is more practical. This sequence can be used to approximate the joint distribution ; to approximate the marginal distribution of one of the variables, or some subset of the variables ; or to compute an integral. Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled.
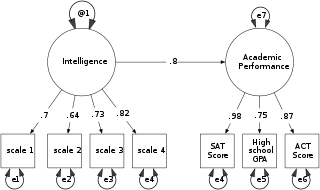
Structural equation modeling (SEM) is a diverse set of methods used by scientists doing both observational and experimental research. SEM is used mostly in the social and behavioral sciences but it is also used in epidemiology, business, and other fields. A definition of SEM is difficult without reference to technical language, but a good starting place is the name itself.
The Rasch model, named after Georg Rasch, is a psychometric model for analyzing categorical data, such as answers to questions on a reading assessment or questionnaire responses, as a function of the trade-off between the respondent's abilities, attitudes, or personality traits, and the item difficulty. For example, they may be used to estimate a student's reading ability or the extremity of a person's attitude to capital punishment from responses on a questionnaire. In addition to psychometrics and educational research, the Rasch model and its extensions are used in other areas, including the health profession, agriculture, and market research.
The polytomous Rasch model is generalization of the dichotomous Rasch model. It is a measurement model that has potential application in any context in which the objective is to measure a trait or ability through a process in which responses to items are scored with successive integers. For example, the model is applicable to the use of Likert scales, rating scales, and to educational assessment items for which successively higher integer scores are intended to indicate increasing levels of competence or attainment.
In statistics, latent variables are variables that can only be inferred indirectly through a mathematical model from other observable variables that can be directly observed or measured. Such latent variable models are used in many disciplines, including engineering, medicine, ecology, physics, machine learning/artificial intelligence, natural language processing, bioinformatics, chemometrics, demography, economics, management, political science, psychology and the social sciences.
In statistics, a latent class model (LCM) is a model for clustering multivariate discrete data. It assumes that the data arise from a mixture of discrete distributions, within each of which the variables are independent. It is called a latent class model because the class to which each data point belongs is unobserved, or latent.
A latent variable model is a statistical model that relates a set of observable variables to a set of latent variables. Latent variable models are applied across a wide range of fields such as biology, computer science, and social science. Common use cases for latent variable models include applications in psychometrics, and natural language processing.
In statistics, multinomial logistic regression is a classification method that generalizes logistic regression to multiclass problems, i.e. with more than two possible discrete outcomes. That is, it is a model that is used to predict the probabilities of the different possible outcomes of a categorically distributed dependent variable, given a set of independent variables.
Multilevel models are statistical models of parameters that vary at more than one level. An example could be a model of student performance that contains measures for individual students as well as measures for classrooms within which the students are grouped. These models can be seen as generalizations of linear models, although they can also extend to non-linear models. These models became much more popular after sufficient computing power and software became available.
Differential item functioning (DIF) is a statistical property of a test item that indicates how likely it is for individuals from distinct groups, possessing similar abilities, to respond differently to the item. It manifests when individuals from different groups, with comparable skill levels, do not have an equal likelihood of answering a question correctly. There are two primary types of DIF: uniform DIF, where one group consistently has an advantage over the other, and nonuniform DIF, where the advantage varies based on the individual's ability level. The presence of DIF requires review and judgment, but it doesn't always signify bias. DIF analysis provides an indication of unexpected behavior of items on a test. DIF characteristic of an item isn't solely determined by varying probabilities of selecting a specific response among individuals from different groups. Rather, DIF becomes pronounced when individuals from different groups, who possess the same underlying true ability, exhibit differing probabilities of giving a certain response. Even when uniform bias is present, test developers sometimes resort to assumptions such as DIF biases may offset each other due to the extensive work required to address it, compromising test ethics and perpetuating systemic biases. Common procedures for assessing DIF are Mantel-Haenszel procedure, logistic regression, item response theory (IRT) based methods, and confirmatory factor analysis (CFA) based methods.
In statistics and econometrics, the multinomial probit model is a generalization of the probit model used when there are several possible categories that the dependent variable can fall into. As such, it is an alternative to the multinomial logit model as one method of multiclass classification. It is not to be confused with the multivariate probit model, which is used to model correlated binary outcomes for more than one independent variable.