Lusser's law

Last updated December 15, 2020

Lusser's law in systems engineering is a prediction of reliability. Named after engineer Robert Lusser,^[1] and also known as Lusser's product law or the probability product law of series components, it states that the reliability of a series of components is equal to the product of the individual reliabilities of the components, if their failure modes are known to be statistically independent. For a series of N components, this is expressed as:^[2]^[3]

R_{s}=\prod _{i=1}^{N}r_{i}=r_{1}\times r_{2}\times r_{3}\times ...\times r_{n}

where R_s is the overall reliability of the system, and r_n is the reliability of the n^th component.

If the failure probabilities of all components are equal, then as Lusser's colleague Erich Pieruschka observed, this can be expressed simply as:^[2]

R_{s}=r^{N}

Lusser's law has been described as the idea that a series system is "weaker than its weakest link", as the product reliability of a series of components can be less than the lowest-value component.^[4]

For example, given a series system of two components with different reliabilities — one of 0.95 and the other of 0.8 — Lusser's law will predict a reliability of

R_{s}=0.95\times 0.8=0.76

which is lower than either of the individual components.

Related Research Articles

There are several kinds of mean in mathematics, especially in statistics.

In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.

In reliability engineering, the term availability has the following meanings:

Unavailability is the probability that an item will not operate correctly at a given time and under specified conditions. It opposes availability.

In statistics, the likelihood function measures the goodness of fit of a statistical model to a sample of data for given values of the unknown parameters. It is formed from the joint probability distribution of the sample, but viewed and used as a function of the parameters only, thus treating the random variables as fixed at the observed values.

Negative binomial distribution Probability distribution

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of successes in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of failures occurs. For example, we can define rolling a 6 on a die as a failure, and rolling any other number as a success, and ask how many successful rolls will occur before we see the third failure. In such a case, the probability distribution of the number of non-6s that appear will be a negative binomial distribution.

Mean time between failures (MTBF) is the predicted elapsed time between inherent failures of a mechanical or electronic system, during normal system operation. MTBF can be calculated as the arithmetic mean (average) time between failures of a system. The term is used for repairable systems, while mean time to failure (MTTF) denotes the expected time to failure for a non-repairable system.

In probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variablesX_i are identically distributed and independent. Prosaically, a Bernoulli process is a repeated coin flipping, possibly with an unfair coin. Every variable X_i in the sequence is associated with a Bernoulli trial or experiment. They all have the same Bernoulli distribution. Much of what can be said about the Bernoulli process can also be generalized to more than two outcomes ; this generalization is known as the Bernoulli scheme.

In probability theory and statistics, the Weibull distribution is a continuous probability distribution. It is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Fréchet (1927) and first applied by Rosin & Rammler (1933) to describe a particle size distribution.

Components of an electrical circuit or electronic circuit can be connected in series, parallel, or series-parallel. The two simplest of these are called series and parallel and occur frequently. Components connected in series are connected along a single conductive path, so the same current flows through all of the components but voltage is dropped (lost) across each of the resistances. In a series circuit, the sum of the voltages consumed by each individual resistance is equal to the source voltage. Components connected in parallel are connected along multiple paths so that the current can split up; the same voltage is applied to each component.

Survival analysis is a branch of statistics for analyzing the expected duration of time until one or more events happen, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory or reliability analysis in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival?

In quantum mechanics, a probability amplitude is a complex number used in describing the behaviour of systems. The modulus squared of this quantity represents a probability or probability density.

Failure rate is the frequency with which an engineered system or component fails, expressed in failures per unit of time. It is usually denoted by the Greek letter λ (lambda) and is often used in reliability engineering.

Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability describes the ability of a system or component to function under stated conditions for a specified period of time. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time.

In engineering, redundancy is the duplication of critical components or functions of a system with the intention of increasing reliability of the system, usually in the form of a backup or fail-safe, or to improve actual system performance, such as in the case of GNSS receivers, or multi-threaded computer processing.

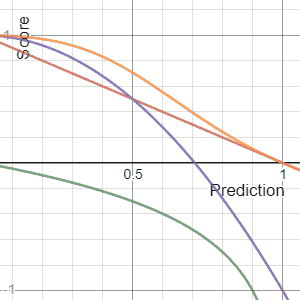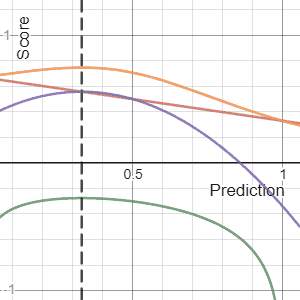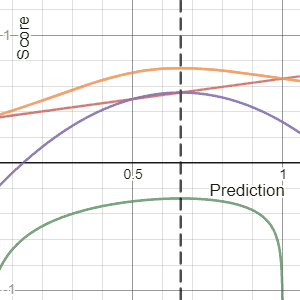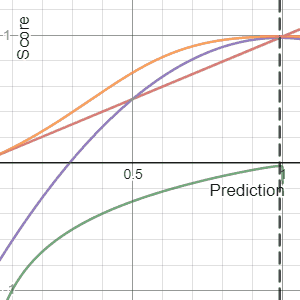
In decision theory, a score function, or scoring rule, measures the accuracy of probabilistic predictions. It is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive outcomes. The set of possible outcomes can be either binary or categorical in nature, and the probabilities assigned to this set of outcomes must sum to one. A score can be thought of as either a measure of the "calibration" of a set of probabilistic predictions, or as a "cost function" or "loss function".

A single point of failure (SPOF) is a part of a system that, if it fails, will stop the entire system from working. SPOFs are undesirable in any system with a goal of high availability or reliability, be it a business practice, software application, or other industrial system.

A reliability block diagram (RBD) is a diagrammatic method for showing how component reliability contributes to the success or failure of a redundant. RBD is also known as a dependence diagram (DD).

The survival function is a function that gives the probability that a patient, device, or other object of interest will survive beyond any specified time.

Maintenance Philosophy is the mix of strategies that ensure an item works as expected when needed.

References

↑ Collins, R. (July 14, 2003). "Lusser's Law". The American Spectator. Retrieved 10 August 2015.
1 2 DeVale, J. (1998). "Basics of Traditional Reliability" (PDF). p. 8. Retrieved 11 August 2015.
↑ Kopp, C. (1996). "System Reliability and Metrics of Reliability" (PDF). Peter Harding & Associates, Pty Ltd. p. 7. Retrieved 11 August 2015.
↑ Critchley, Terry (2014). High Availability IT Services. CRC Press. p. 117. ISBN 9781482255911.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[AmSpec-1] Collins, R. (July 14, 2003). "Lusser's Law". The American Spectator. Retrieved 10 August 2015.

[DeVale-2] 1 2 DeVale, J. (1998). "Basics of Traditional Reliability" (PDF). p. 8. Retrieved 11 August 2015.

[Kopp-3] Kopp, C. (1996). "System Reliability and Metrics of Reliability" (PDF). Peter Harding & Associates, Pty Ltd. p. 7. Retrieved 11 August 2015.

[Critchley-4] Critchley, Terry (2014). High Availability IT Services. CRC Press. p. 117. ISBN 9781482255911.

[1]

[2]

[3]

[4]