Waiting time distribution
Erlang showed that when ρ = (λ D)/c < 1, the waiting time distribution has distribution F(y) given by [4]
Crommelin showed that, writing Pn for the stationary probability of a system with n or fewer customers, [5]
In queueing theory, a discipline within the mathematical theory of probability, an M/D/c queue represents the queue length in a system having c servers, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. [1] Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. [2] [3] The model is an extension of the M/D/1 queue which has only a single server.
An M/D/c queue is a stochastic process whose state space is the set {0,1,2,3,...} where the value corresponds to the number of customers in the system, including any currently in service.
Erlang showed that when ρ = (λ D)/c < 1, the waiting time distribution has distribution F(y) given by [4]
Crommelin showed that, writing Pn for the stationary probability of a system with n or fewer customers, [5]
The erlang is a dimensionless unit that is used in telephony as a measure of offered load or carried load on service-providing elements such as telephone circuits or telephone switching equipment. A single cord circuit has the capacity to be used for 60 minutes in one hour. Full utilization of that capacity, 60 minutes of traffic, constitutes 1 erlang.

Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.
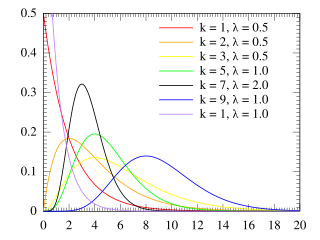
The Erlang distribution is a two-parameter family of continuous probability distributions with support . The two parameters are:
In probability theory the hypoexponential distribution or the generalized Erlang distribution is a continuous distribution, that has found use in the same fields as the Erlang distribution, such as queueing theory, teletraffic engineering and more generally in stochastic processes. It is called the hypoexponetial distribution as it has a coefficient of variation less than one, compared to the hyper-exponential distribution which has coefficient of variation greater than one and the exponential distribution which has coefficient of variation of one.
In queueing theory, a discipline within the mathematical theory of probability, a Jackson network is a class of queueing network where the equilibrium distribution is particularly simple to compute as the network has a product-form solution. It was the first significant development in the theory of networks of queues, and generalising and applying the ideas of the theorem to search for similar product-form solutions in other networks has been the subject of much research, including ideas used in the development of the Internet. The networks were first identified by James R. Jackson and his paper was re-printed in the journal Management Science’s ‘Ten Most Influential Titles of Management Sciences First Fifty Years.’
In probability theory, the Lindley equation, Lindley recursion or Lindley processes is a discrete-time stochastic process An where n takes integer values and:
A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the states of the Markov process represents one of the phases.
In queueing theory, a discipline within the mathematical theory of probability, the Pollaczek–Khinchine formula states a relationship between the queue length and service time distribution Laplace transforms for an M/G/1 queue. The term is also used to refer to the relationships between the mean queue length and mean waiting/service time in such a model.

In queueing theory, a discipline within the mathematical theory of probability, an M/M/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times have an exponential distribution. The model name is written in Kendall's notation. The model is the most elementary of queueing models and an attractive object of study as closed-form expressions can be obtained for many metrics of interest in this model. An extension of this model with more than one server is the M/M/c queue.

In queueing theory, a discipline within the mathematical theory of probability, a fork–join queue is a queue where incoming jobs are split on arrival for service by numerous servers and joined before departure. The model is often used for parallel computations or systems where products need to be obtained simultaneously from different suppliers. The key quantity of interest in this model is usually the time taken to service a complete job. The model has been described as a "key model for the performance analysis of parallel and distributed systems." Few analytical results exist for fork–join queues, but various approximations are known.

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson. The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume. It plays an important role for discrete-stable distributions.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/c queue is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a Poisson process, there are c servers, and job service times are exponentially distributed. It is a generalisation of the M/M/1 queue which considers only a single server. The model with infinitely many servers is the M/M/∞ queue.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/k queue is a queue model where arrivals are Markovian, service times have a General distribution and there are k servers. The model name is written in Kendall's notation, and is an extension of the M/M/c queue, where service times must be exponentially distributed and of the M/G/1 queue with a single server. Most performance metrics for this queueing system are not known and remain an open problem.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/∞ queue is a multi-server queueing model where every arrival experiences immediate service and does not wait. In Kendall's notation it describes a system where arrivals are governed by a Poisson process, there are infinitely many servers, so jobs do not need to wait for a server. Each job has an exponentially distributed service time. It is a limit of the M/M/c queue model where the number of servers c becomes very large.
In queueing theory, a discipline within the mathematical theory of probability, a heavy traffic approximation is the matching of a queueing model with a diffusion process under some limiting conditions on the model's parameters. The first such result was published by John Kingman who showed that when the utilisation parameter of an M/M/1 queue is near 1 a scaled version of the queue length process can be accurately approximated by a reflected Brownian motion.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue.
In queueing theory, a discipline within the mathematical theory of probability, a D/M/1 queue represents the queue length in a system having a single server, where arrivals occur at fixed regular intervals and job service requirements are random with an exponential distribution. The model name is written in Kendall's notation. Agner Krarup Erlang first published a solution to the stationary distribution of a D/M/1 and D/M/k queue, the model with k servers, in 1917 and 1920.
In queueing theory, a discipline within the mathematical theory of probability, a Kelly network is a general multiclass queueing network. In the network each node is quasireversible and the network has a product-form stationary distribution, much like the single-class Jackson network.
In queueing theory, a discipline within the mathematical theory of probability, the G/M/1 queue represents the queue length in a system where interarrival times have a general distribution and service times for each job have an exponential distribution. The system is described in Kendall's notation where the G denotes a general distribution, M the exponential distribution for service times and the 1 that the model has a single server.