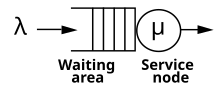
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service.
In probability theory, the Vysochanskij–Petunin inequality gives a lower bound for the probability that a random variable with finite variance lies within a certain number of standard deviations of the variable's mean, or equivalently an upper bound for the probability that it lies further away. The sole restrictions on the distribution are that it be unimodal and have finite variance.
The birth–death process is a special case of continuous-time Markov process where the state transitions are of only two types: "births", which increase the state variable by one and "deaths", which decrease the state by one. It was introduced by William Feller. The model's name comes from a common application, the use of such models to represent the current size of a population where the transitions are literal births and deaths. Birth–death processes have many applications in demography, queueing theory, performance engineering, epidemiology, biology and other areas. They may be used, for example, to study the evolution of bacteria, the number of people with a disease within a population, or the number of customers in line at the supermarket.
In probability theory and statistics, the noncentral chi distribution is a noncentral generalization of the chi distribution. It is also known as the generalized Rayleigh distribution.
In queueing theory, a discipline within the mathematical theory of probability, a Jackson network is a class of queueing network where the equilibrium distribution is particularly simple to compute as the network has a product-form solution. It was the first significant development in the theory of networks of queues, and generalising and applying the ideas of the theorem to search for similar product-form solutions in other networks has been the subject of much research, including ideas used in the development of the Internet. The networks were first identified by James R. Jackson and his paper was re-printed in the journal Management Science’s ‘Ten Most Influential Titles of Management Sciences First Fifty Years.’
In quantum information theory, quantum relative entropy is a measure of distinguishability between two quantum states. It is the quantum mechanical analog of relative entropy.
Bayesian linear regression is a type of conditional modeling in which the mean of one variable is described by a linear combination of other variables, with the goal of obtaining the posterior probability of the regression coefficients and ultimately allowing the out-of-sample prediction of the regressandconditional on observed values of the regressors. The simplest and most widely used version of this model is the normal linear model, in which given is distributed Gaussian. In this model, and under a particular choice of prior probabilities for the parameters—so-called conjugate priors—the posterior can be found analytically. With more arbitrarily chosen priors, the posteriors generally have to be approximated.
A ratio distribution is a probability distribution constructed as the distribution of the ratio of random variables having two other known distributions. Given two random variables X and Y, the distribution of the random variable Z that is formed as the ratio Z = X/Y is a ratio distribution.
In queueing theory, a discipline within the mathematical theory of probability, a G-network is an open network of G-queues first introduced by Erol Gelenbe as a model for queueing systems with specific control functions, such as traffic re-routing or traffic destruction, as well as a model for neural networks. A G-queue is a network of queues with several types of novel and useful customers:
In queueing theory, a discipline within the mathematical theory of probability, the Pollaczek–Khinchine formula states a relationship between the queue length and service time distribution Laplace transforms for an M/G/1 queue. The term is also used to refer to the relationships between the mean queue length and mean waiting/service time in such a model.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/c queue is a multi-server queueing model. In Kendall's notation it describes a system where arrivals form a single queue and are governed by a Poisson process, there are c servers, and job service times are exponentially distributed. It is a generalisation of the M/M/1 queue which considers only a single server. The model with infinitely many servers is the M/M/∞ queue.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
In queueing theory, a discipline within the mathematical theory of probability, a fluid queue is a mathematical model used to describe the fluid level in a reservoir subject to randomly determined periods of filling and emptying. The term dam theory was used in earlier literature for these models. The model has been used to approximate discrete models, model the spread of wildfires, in ruin theory and to model high speed data networks. The model applies the leaky bucket algorithm to a stochastic source.
In queueing theory, a discipline within the mathematical theory of probability, the M/M/∞ queue is a multi-server queueing model where every arrival experiences immediate service and does not wait. In Kendall's notation it describes a system where arrivals are governed by a Poisson process, there are infinitely many servers, so jobs do not need to wait for a server. Each job has an exponentially distributed service time. It is a limit of the M/M/c queue model where the number of servers c becomes very large.
In queueing theory, a discipline within the mathematical theory of probability, a heavy traffic approximation is the matching of a queueing model with a diffusion process under some limiting conditions on the model's parameters. The first such result was published by John Kingman who showed that when the utilisation parameter of an M/M/1 queue is near 1 a scaled version of the queue length process can be accurately approximated by a reflected Brownian motion.
In probability theory and statistics, the generalized multivariate log-gamma (G-MVLG) distribution is a multivariate distribution introduced by Demirhan and Hamurkaroglu in 2011. The G-MVLG is a flexible distribution. Skewness and kurtosis are well controlled by the parameters of the distribution. This enables one to control dispersion of the distribution. Because of this property, the distribution is effectively used as a joint prior distribution in Bayesian analysis, especially when the likelihood is not from the location-scale family of distributions such as normal distribution.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/1 queue represents the queue length in a system having a single server, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. An extension of this model with more than one server is the M/D/c queue.
In queueing theory, a discipline within the mathematical theory of probability, an M/D/c queue represents the queue length in a system having c servers, where arrivals are determined by a Poisson process and job service times are fixed (deterministic). The model name is written in Kendall's notation. Agner Krarup Erlang first published on this model in 1909, starting the subject of queueing theory. The model is an extension of the M/D/1 queue which has only a single server.
In queueing theory, a discipline within the mathematical theory of probability, the G/M/1 queue represents the queue length in a system where interarrival times have a general distribution and service times for each job have an exponential distribution. The system is described in Kendall's notation where the G denotes a general distribution, M the exponential distribution for service times and the 1 that the model has a single server.

The Queuing Rule of Thumb (QROT) is a mathematical formula, known as the queuing constraint equation when it is used to find an approximation of servers required to service a queue. The formula is written as an inequality relating the number of servers (s), total number of service requestors (N), service time (r), and the maximum time to empty the queue (T):