In computer science, an array is a data structure consisting of a collection of elements, of same memory size, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called a one-dimensional array.

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.
A histogram is a visual representation of the distribution of quantitative data. To construct a histogram, the first step is to "bin" the range of values— divide the entire range of values into a series of intervals—and then count how many values fall into each interval. The bins are usually specified as consecutive, non-overlapping intervals of a variable. The bins (intervals) are adjacent and are typically of equal size.

A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable-length output. The values returned by a hash function are called hash values, hash codes, hash digests, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter-storage addressing.

In computer science and information theory, a Huffman code is a particular type of optimal prefix code that is commonly used for lossless data compression. The process of finding or using such a code is Huffman coding, an algorithm developed by David A. Huffman while he was a Sc.D. student at MIT, and published in the 1952 paper "A Method for the Construction of Minimum-Redundancy Codes".

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

Bucket sort, or bin sort, is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm. It is a distribution sort, a generalization of pigeonhole sort that allows multiple keys per bucket, and is a cousin of radix sort in the most-to-least significant digit flavor. Bucket sort can be implemented with comparisons and therefore can also be considered a comparison sort algorithm. The computational complexity depends on the algorithm used to sort each bucket, the number of buckets to use, and whether the input is uniformly distributed.
A* is a graph traversal and pathfinding algorithm that is used in many fields of computer science due to its completeness, optimality, and optimal efficiency. Given a weighted graph, a source node and a goal node, the algorithm finds the shortest path from source to goal.
Alpha–beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player combinatorial games. It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.
Template metaprogramming (TMP) is a metaprogramming technique in which templates are used by a compiler to generate temporary source code, which is merged by the compiler with the rest of the source code and then compiled. The output of these templates can include compile-time constants, data structures, and complete functions. The use of templates can be thought of as compile-time polymorphism. The technique is used by a number of languages, the best-known being C++, but also Curl, D, Nim, and XL.
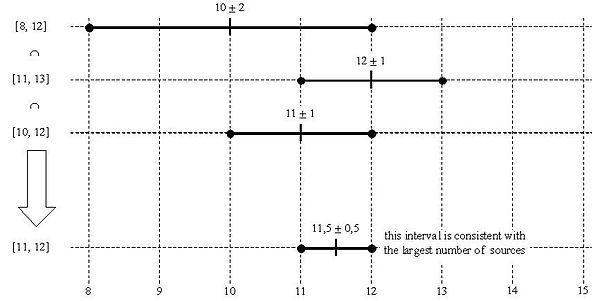
The intersection algorithm is an agreement algorithm used to select sources for estimating accurate time from a number of noisy time sources. It forms part of the modern Network Time Protocol. It is a modified form of Marzullo's algorithm.
In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.
In computer science, an interval tree is a tree data structure to hold intervals. Specifically, it allows one to efficiently find all intervals that overlap with any given interval or point. It is often used for windowing queries, for instance, to find all roads on a computerized map inside a rectangular viewport, or to find all visible elements inside a three-dimensional scene. A similar data structure is the segment tree.

Quicksort is an efficient, general-purpose sorting algorithm. Quicksort was developed by British computer scientist Tony Hoare in 1959 and published in 1961. It is still a commonly used algorithm for sorting. Overall, it is slightly faster than merge sort and heapsort for randomized data, particularly on larger distributions.
Query optimization is a feature of many relational database management systems and other databases such as NoSQL and graph databases. The query optimizer attempts to determine the most efficient way to execute a given query by considering the possible query plans.
Interval scheduling is a class of problems in computer science, particularly in the area of algorithm design. The problems consider a set of tasks. Each task is represented by an interval describing the time in which it needs to be processed by some machine. For instance, task A might run from 2:00 to 5:00, task B might run from 4:00 to 10:00 and task C might run from 9:00 to 11:00. A subset of intervals is compatible if no two intervals overlap on the machine/resource. For example, the subset {A,C} is compatible, as is the subset {B}; but neither {A,B} nor {B,C} are compatible subsets, because the corresponding intervals within each subset overlap.
Histograms are most commonly used as visual representations of data. However, Database systems use histograms to summarize data internally and provide size estimates for queries. These histograms are not presented to users or displayed visually, so a wider range of options are available for their construction. Simple or exotic histograms are defined by four parameters, Sort Value, Source Value, Partition Class and Partition Rule. The most basic histogram is the equi-width histogram, where each bucket represents the same range of values. That histogram would be defined as having a Sort Value of Value, a Source Value of Frequency, be in the Serial Partition Class and have a Partition Rule stating that all buckets have the same range.
The activity selection problem is a combinatorial optimization problem concerning the selection of non-conflicting activities to perform within a given time frame, given a set of activities each marked by a start time (si) and finish time (fi). The problem is to select the maximum number of activities that can be performed by a single person or machine, assuming that a person can only work on a single activity at a time. The activity selection problem is also known as the Interval scheduling maximization problem (ISMP), which is a special type of the more general Interval Scheduling problem.
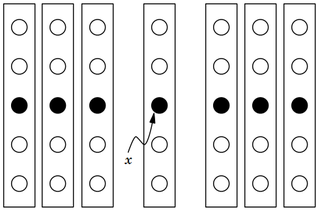
In computer science, the median of medians is an approximate median selection algorithm, frequently used to supply a good pivot for an exact selection algorithm, most commonly quickselect, that selects the kth smallest element of an initially unsorted array. Median of medians finds an approximate median in linear time. Using this approximate median as an improved pivot, the worst-case complexity of quickselect reduces from quadratic to linear, which is also the asymptotically optimal worst-case complexity of any selection algorithm. In other words, the median of medians is an approximate median-selection algorithm that helps building an asymptotically optimal, exact general selection algorithm, by producing good pivot elements.