
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. It is the study of numerical methods that attempt to find approximate solutions of problems rather than the exact ones. Numerical analysis finds application in all fields of engineering and the physical sciences, and in the 21st century also the life and social sciences like economics, medicine, business and even the arts. Current growth in computing power has enabled the use of more complex numerical analysis, providing detailed and realistic mathematical models in science and engineering. Examples of numerical analysis include: ordinary differential equations as found in celestial mechanics, numerical linear algebra in data analysis, and stochastic differential equations and Markov chains for simulating living cells in medicine and biology.
Natural language processing (NLP) is a subfield of computer science and especially artificial intelligence. It is primarily concerned with providing computers with the ability to process data encoded in natural language and is thus closely related to information retrieval, knowledge representation and computational linguistics, a subfield of linguistics. Typically data is collected in text corpora, using either rule-based, statistical or neural-based approaches in machine learning and deep learning.

A cladogram is a diagram used in cladistics to show relations among organisms. A cladogram is not, however, an evolutionary tree because it does not show how ancestors are related to descendants, nor does it show how much they have changed, so many differing evolutionary trees can be consistent with the same cladogram. A cladogram uses lines that branch off in different directions ending at a clade, a group of organisms with a last common ancestor. There are many shapes of cladograms but they all have lines that branch off from other lines. The lines can be traced back to where they branch off. These branching off points represent a hypothetical ancestor which can be inferred to exhibit the traits shared among the terminal taxa above it. This hypothetical ancestor might then provide clues about the order of evolution of various features, adaptation, and other evolutionary narratives about ancestors. Although traditionally such cladograms were generated largely on the basis of morphological characters, DNA and RNA sequencing data and computational phylogenetics are now very commonly used in the generation of cladograms, either on their own or in combination with morphology.
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, source reconstruction in acoustics, or calculating the density of the Earth from measurements of its gravity field. It is called an inverse problem because it starts with the effects and then calculates the causes. It is the inverse of a forward problem, which starts with the causes and then calculates the effects.
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus "error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models.

Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests.
Structural analysis is a branch of solid mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on physical structures and their components. In contrast to theory of elasticity, the models used in structural analysis are often differential equations in one spatial variable. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, aircraft and ships. Structural analysis uses ideas from applied mechanics, materials science and applied mathematics to compute a structure's deformations, internal forces, stresses, support reactions, velocity, accelerations, and stability. The results of the analysis are used to verify a structure's fitness for use, often precluding physical tests. Structural analysis is thus a key part of the engineering design of structures.

Fritz Zwicky was a Swiss astronomer. He worked most of his life at the California Institute of Technology in the United States of America, where he made many important contributions in theoretical and observational astronomy. In 1933, Zwicky was the first to use the virial theorem to postulate the existence of unseen dark matter, describing it as "dunkle Materie".

Morphological analysis or general morphological analysis is a method for exploring possible solutions to a multi-dimensional, non-quantified complex problem. It was developed by Swiss astronomer Fritz Zwicky. General morphology has found use in fields including engineering design, technological forecasting, organizational development and policy analysis.
In electrical engineering and electronics, a network is a collection of interconnected components. Network analysis is the process of finding the voltages across, and the currents through, all network components. There are many techniques for calculating these values; however, for the most part, the techniques assume linear components. Except where stated, the methods described in this article are applicable only to linear network analysis.

Tired light is a class of hypothetical redshift mechanisms that was proposed as an alternative explanation for the redshift-distance relationship. These models have been proposed as alternatives to the models that involve the expansion of the universe. The concept was first proposed in 1929 by Fritz Zwicky, who suggested that if photons lost energy over time through collisions with other particles in a regular way, the more distant objects would appear redder than more nearby ones.
In phylogenetics and computational phylogenetics, maximum parsimony is an optimality criterion under which the phylogenetic tree that minimizes the total number of character-state changes. Under the maximum-parsimony criterion, the optimal tree will minimize the amount of homoplasy. In other words, under this criterion, the shortest possible tree that explains the data is considered best. Some of the basic ideas behind maximum parsimony were presented by James S. Farris in 1970 and Walter M. Fitch in 1971.
In planning and policy, a wicked problem is a problem that is difficult or impossible to solve because of incomplete, contradictory, and changing requirements that are often difficult to recognize. It refers to an idea or problem that cannot be fixed, where there is no single solution to the problem; and "wicked" denotes resistance to resolution, rather than evil. Another definition is "a problem whose social complexity means that it has no determinable stopping point". Moreover, because of complex interdependencies, the effort to solve one aspect of a wicked problem may reveal or create other problems. Due to their complexity, wicked problems are often characterized by organized irresponsibility.
In numerical analysis, a multigrid method is an algorithm for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior. For example, many basic relaxation methods exhibit different rates of convergence for short- and long-wavelength components, suggesting these different scales be treated differently, as in a Fourier analysis approach to multigrid. MG methods can be used as solvers as well as preconditioners.
Futures techniques used in the multi-disciplinary field of futurology by futurists in Americas and Australasia, and futurology by futurologists in EU, include a diverse range of forecasting methods, including anticipatory thinking, backcasting, simulation, and visioning. Some of the anticipatory methods include, the delphi method, causal layered analysis, environmental scanning, morphological analysis, and scenario planning.
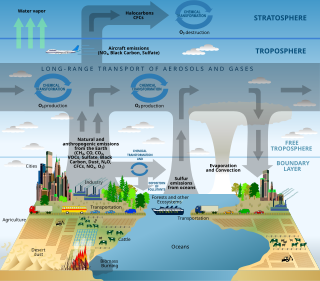
Scientific modelling is an activity that produces models representing empirical objects, phenomena, and physical processes, to make a particular part or feature of the world easier to understand, define, quantify, visualize, or simulate. It requires selecting and identifying relevant aspects of a situation in the real world and then developing a model to replicate a system with those features. Different types of models may be used for different purposes, such as conceptual models to better understand, operational models to operationalize, mathematical models to quantify, computational models to simulate, and graphical models to visualize the subject.
Computational phylogenetics, phylogeny inference, or phylogenetic inference focuses on computational and optimization algorithms, heuristics, and approaches involved in phylogenetic analyses. The goal is to find a phylogenetic tree representing optimal evolutionary ancestry between a set of genes, species, or taxa. Maximum likelihood, parsimony, Bayesian, and minimum evolution are typical optimality criteria used to assess how well a phylogenetic tree topology describes the sequence data. Nearest Neighbour Interchange (NNI), Subtree Prune and Regraft (SPR), and Tree Bisection and Reconnection (TBR), known as tree rearrangements, are deterministic algorithms to search for optimal or the best phylogenetic tree. The space and the landscape of searching for the optimal phylogenetic tree is known as phylogeny search space.
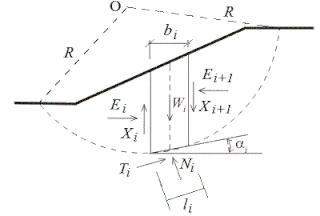
Slope stability analysis is a static or dynamic, analytical or empirical method to evaluate the stability of slopes of soil- and rock-fill dams, embankments, excavated slopes, and natural slopes in soil and rock. It is performed to assess the safe design of a human-made or natural slopes and the equilibrium conditions. Slope stability is the resistance of inclined surface to failure by sliding or collapsing. The main objectives of slope stability analysis are finding endangered areas, investigation of potential failure mechanisms, determination of the slope sensitivity to different triggering mechanisms, designing of optimal slopes with regard to safety, reliability and economics, and designing possible remedial measures, e.g. barriers and stabilization.
In computational engineering, Luus–Jaakola (LJ) denotes a heuristic for global optimization of a real-valued function. In engineering use, LJ is not an algorithm that terminates with an optimal solution; nor is it an iterative method that generates a sequence of points that converges to an optimal solution. However, when applied to a twice continuously differentiable function, the LJ heuristic is a proper iterative method, that generates a sequence that has a convergent subsequence; for this class of problems, Newton's method is recommended and enjoys a quadratic rate of convergence, while no convergence rate analysis has been given for the LJ heuristic. In practice, the LJ heuristic has been recommended for functions that need be neither convex nor differentiable nor locally Lipschitz: The LJ heuristic does not use a gradient or subgradient when one be available, which allows its application to non-differentiable and non-convex problems.








