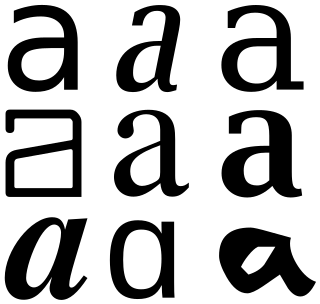
In linguistics, a grapheme is the smallest functional unit of a writing system. The word grapheme is derived from Ancient Greek γράφω (gráphō) 'write' and the suffix -eme by analogy with phoneme and other names of emic units. The study of graphemes is called graphemics. The concept of graphemes is abstract and similar to the notion in computing of a character. By comparison, a specific shape that represents any particular grapheme in a given typeface is called a glyph.

In mathematics, the power set (or powerset) of a set S is the set of all subsets of S, including the empty set and S itself. In axiomatic set theory (as developed, for example, in the ZFC axioms), the existence of the power set of any set is postulated by the axiom of power set. The powerset of S is variously denoted as P(S), 𝒫(S), P(S), , , or 2S. The notation 2S, meaning the set of all functions from S to a given set of two elements (e.g., {0, 1}), is used because the powerset of S can be identified with, equivalent to, or bijective to the set of all the functions from S to the given two elements set.
ANSI escape sequences are a standard for in-band signaling to control cursor location, color, font styling, and other options on video text terminals and terminal emulators. Certain sequences of bytes, most starting with an ASCII escape character and a bracket character, are embedded into text. The terminal interprets these sequences as commands, rather than text to display verbatim.

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
A trigraph is a group of three characters used to represent a single sound or a combination of sounds that does not correspond to the written letters combined.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).

In graph theory, a proper edge coloring of a graph is an assignment of "colors" to the edges of the graph so that no two incident edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several different types of graph coloring. The edge-coloring problem asks whether it is possible to color the edges of a given graph using at most k different colors, for a given value of k, or with the fewest possible colors. The minimum required number of colors for the edges of a given graph is called the chromatic index of the graph. For example, the edges of the graph in the illustration can be colored by three colors but cannot be colored by two colors, so the graph shown has chromatic index three.

In graph theory, the degree of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex is denoted or . The maximum degree of a graph , denoted by , and the minimum degree of a graph, denoted by , are the maximum and minimum of its vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0.

In mathematics, and more specifically in graph theory, a multigraph is a graph which is permitted to have multiple edges, that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge.

An addressograph is an address labeler and labeling system.
A tetragraph is a sequence of four letters used to represent a single sound (phoneme), or a combination of sounds, that do not necessarily correspond to the individual values of the letters. In German, for example, the tetragraph tsch represents the sound of the English digraph ch. English does not have tetragraphs in native words, but chth is a true tetragraph when found initially in words of Greek origin such as chthonian.
Graphemics or graphematics is the linguistic study of writing systems and their basic components, i.e. graphemes.
A multigraph is a sequence of letters that behaves as a unit and is not the sum of its parts, such as English ⟨ch⟩ or French ⟨eau⟩. The term is infrequently used, as the number of letters is usually specified:

In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by directed edges, often called arcs.
A heptagraph is a sequence of seven letters used to represent a single sound (phoneme), or a combination of sounds, that do not correspond to the individual values of the letters.
A Latin-script multigraph is a multigraph consisting of characters of the Latin script.
A sparsity matroid is a mathematical structure that captures how densely a multigraph is populated with edges. To unpack this a little, sparsity is a measure of density of a graph that bounds the number of edges in any subgraph. The property of having a particular matroid as its density measure is invariant under graph isomorphisms and so it is a graph invariant.