
In mathematics, fractal is a term used to describe geometric shapes containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set. This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar. Fractal geometry lies within the mathematical branch of measure theory.
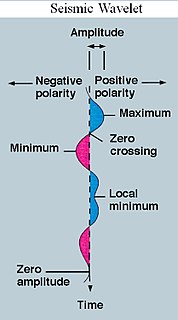
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
In time series analysis, dynamic time warping (DTW) is an algorithm for measuring similarity between two temporal sequences, which may vary in speed. For instance, similarities in walking could be detected using DTW, even if one person was walking faster than the other, or if there were accelerations and decelerations during the course of an observation. DTW has been applied to temporal sequences of video, audio, and graphics data — indeed, any data that can be turned into a linear sequence can be analyzed with DTW. A well-known application has been automatic speech recognition, to cope with different speaking speeds. Other applications include speaker recognition and online signature recognition. It can also be used in partial shape matching applications.
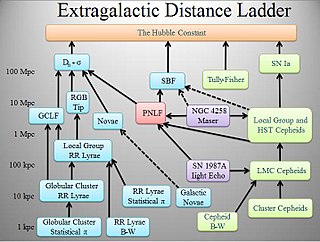
The cosmic distance ladder is the succession of methods by which astronomers determine the distances to celestial objects. A real direct distance measurement of an astronomical object is possible only for those objects that are "close enough" to Earth. The techniques for determining distances to more distant objects are all based on various measured correlations between methods that work at close distances and methods that work at larger distances. Several methods rely on a standard candle, which is an astronomical object that has a known luminosity.

In digital image processing and computer vision, image segmentation is the process of partitioning a digital image into multiple image segments, also known as image regions or image objects. The goal of segmentation is to simplify and/or change the representation of an image into something that is more meaningful and easier to analyze. Image segmentation is typically used to locate objects and boundaries in images. More precisely, image segmentation is the process of assigning a label to every pixel in an image such that pixels with the same label share certain characteristics.
In computational modelling, multiphysics simulation is defined as the simultaneous simulation of different aspects of a physical system or systems. For example, simultaneous simulation of the physical stress on an object and the temperature distribution of the object would be considered a multiphysics simulation. Multiphysics simulation is related to multiscale simulation, which is the simultaneous simulation of a single process on either multiple time or distance scales.

Non-negative matrix factorization, also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements. This non-negativity makes the resulting matrices easier to inspect. Also, in applications such as processing of audio spectrograms or muscular activity, non-negativity is inherent to the data being considered. Since the problem is not exactly solvable in general, it is commonly approximated numerically.

Matching pursuit (MP) is a sparse approximation algorithm which finds the "best matching" projections of multidimensional data onto the span of an over-complete dictionary . The basic idea is to approximately represent a signal from Hilbert space as a weighted sum of finitely many functions taken from . An approximation with atoms has the form

A multifractal system is a generalization of a fractal system in which a single exponent is not enough to describe its dynamics; instead, a continuous spectrum of exponents is needed.
Compressed sensing is a signal processing technique for efficiently acquiring and reconstructing a signal, by finding solutions to underdetermined linear systems. This is based on the principle that, through optimization, the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem. There are two conditions under which recovery is possible. The first one is sparsity, which requires the signal to be sparse in some domain. The second one is incoherence, which is applied through the isometric property, which is sufficient for sparse signals.
Contourlets form a multiresolution directional tight frame designed to efficiently approximate images made of smooth regions separated by smooth boundaries. The contourlet transform has a fast implementation based on a Laplacian pyramid decomposition followed by directional filterbanks applied on each bandpass subband.
Sparse approximation theory deals with sparse solutions for systems of linear equations. Techniques for finding these solutions and exploiting them in applications have found wide use in image processing, signal processing, machine learning, medical imaging, and more.

A Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages. The PageRank of each page can then be generated iteratively from the Google matrix using the power method. However, in order for the power method to converge, the matrix must be stochastic, irreducible and aperiodic.
In linear algebra, the coherence or mutual coherence of a matrix A is defined as the maximum absolute value of the cross-correlations between the columns of A.
Speckle is a granular interference that inherently exists in and degrades the quality of the active radar, synthetic aperture radar (SAR), medical ultrasound and optical coherence tomography images.
Human dynamics refer to a branch of complex systems research in statistical physics such as the movement of crowds and queues and other systems of complex human interactions including statistical modelling of human networks, including interactions over communications networks.
David Leigh Donoho is an American statistician. He is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences. His work includes the development of effective methods for the construction of low-dimensional representations for high-dimensional data problems, development of wavelets for denoising and compressed sensing. He was elected a Member of the American Philosophical Society in 2019.

Diffusion maps is a dimensionality reduction or feature extraction algorithm introduced by Coifman and Lafon which computes a family of embeddings of a data set into Euclidean space whose coordinates can be computed from the eigenvectors and eigenvalues of a diffusion operator on the data. The Euclidean distance between points in the embedded space is equal to the "diffusion distance" between probability distributions centered at those points. Different from linear dimensionality reduction methods such as principal component analysis (PCA), diffusion maps is part of the family of nonlinear dimensionality reduction methods which focus on discovering the underlying manifold that the data has been sampled from. By integrating local similarities at different scales, diffusion maps give a global description of the data-set. Compared with other methods, the diffusion map algorithm is robust to noise perturbation and computationally inexpensive.

Sparse coding is a representation learning method which aims at finding a sparse representation of the input data in the form of a linear combination of basic elements as well as those basic elements themselves. These elements are called atoms and they compose a dictionary. Atoms in the dictionary are not required to be orthogonal, and they may be an over-complete spanning set. This problem setup also allows the dimensionality of the signals being represented to be higher than the one of the signals being observed. The above two properties lead to having seemingly redundant atoms that allow multiple representations of the same signal but also provide an improvement in sparsity and flexibility of the representation.
Probabilistic numerics is a scientific field at the intersection of statistics, machine learning and applied mathematics, where tasks in numerical analysis including finding numerical solutions for integration, linear algebra, optimisation and differential equations are seen as problems of statistical, probabilistic, or Bayesian inference.









