An integer is the number zero (0), a positive natural number, or the negation of a positive natural number. The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set of all integers is often denoted by the boldface Z or blackboard bold .
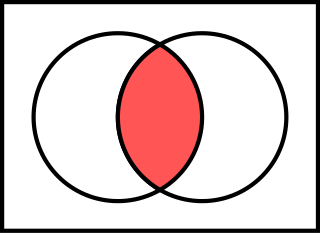
In logic, mathematics and linguistics, and is the truth-functional operator of conjunction or logical conjunction. The logical connective of this operator is typically represented as or or (prefix) or or in which is the most modern and widely used.
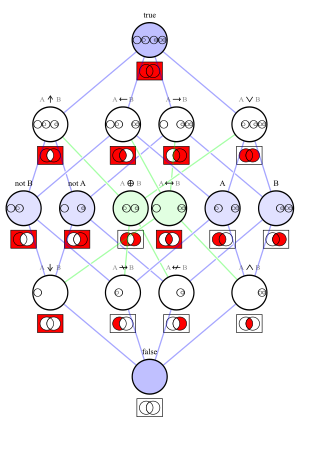
In logic, a logical connective is a logical constant. Connectives can be used to connect logical formulas. For instance in the syntax of propositional logic, the binary connective can be used to join the two atomic formulas and , rendering the complex formula .
Many-valued logic is a propositional calculus in which there are more than two truth values. Traditionally, in Aristotle's logical calculus, there were only two possible values for any proposition. Classical two-valued logic may be extended to n-valued logic for n greater than 2. Those most popular in the literature are three-valued, four-valued, nine-valued, the finite-valued with more than three values, and the infinite-valued (infinitely-many-valued), such as fuzzy logic and probability logic.
Classical logic or Frege–Russell logic is the intensively studied and most widely used class of deductive logic. Classical logic has had much influence on analytic philosophy.

In propositional logic and Boolean algebra, De Morgan's laws, also known as De Morgan's theorem, are a pair of transformation rules that are both valid rules of inference. They are named after Augustus De Morgan, a 19th-century British mathematician. The rules allow the expression of conjunctions and disjunctions purely in terms of each other via negation.

Exclusive or, exclusive disjunction, exclusive alternation, logical non-equivalence, or logical inequality is a logical operator whose negation is the logical biconditional. With two inputs, XOR is true if and only if the inputs differ. With multiple inputs, XOR is true if and only if the number of true inputs is odd.

In logic, negation, also called the logical not or logical complement, is an operation that takes a proposition to another proposition "not ", written , , or . It is interpreted intuitively as being true when is false, and false when is true. For example, if is "Spot runs", then "not " is "Spot does not run". An operand of a negation is called a negand or negatum.
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values.

In Boolean logic, logical NOR, non-disjunction, or joint denial is a truth-functional operator which produces a result that is the negation of logical or. That is, a sentence of the form (p NOR q) is true precisely when neither p nor q is true—i.e. when both p and q are false. It is logically equivalent to and , where the symbol signifies logical negation, signifies OR, and signifies AND.
Any kind of logic, function, expression, or theory based on the work of George Boole is considered Boolean.
In logic, a three-valued logic is any of several many-valued logic systems in which there are three truth values indicating true, false, and some third value. This is contrasted with the more commonly known bivalent logics which provide only for true and false.
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy. LoF describes three distinct logical systems:

In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set. Alternative names are switching function, used especially in older computer science literature, and truth function, used in logic. Boolean functions are the subject of Boolean algebra and switching theory.

In computer science, the Boolean is a data type that has one of two possible values which is intended to represent the two truth values of logic and Boolean algebra. It is named after George Boole, who first defined an algebraic system of logic in the mid 19th century. The Boolean data type is primarily associated with conditional statements, which allow different actions by changing control flow depending on whether a programmer-specified Boolean condition evaluates to true or false. It is a special case of a more general logical data type—logic does not always need to be Boolean.
In mathematics and abstract algebra, the two-element Boolean algebra is the Boolean algebra whose underlying setB is the Boolean domain. The elements of the Boolean domain are 1 and 0 by convention, so that B = {0, 1}. Paul Halmos's name for this algebra "2" has some following in the literature, and will be employed here.

Logical equality is a logical operator that compares two truth values, or more generally, two formulas, such that it gives the value True if both arguments have the same truth value, and False if they are different. In the case where formulas have free variables, we say two formulas are equal when their truth values are equal for all possible resolutions of free variables. It corresponds to equality in Boolean algebra and to the logical biconditional in propositional calculus.

Material nonimplication or abjunction is a term referring to a logic operation used in generic circuits and Boolean algebra. It is the negation of material implication. That is to say that for any two propositions and , the material nonimplication from to is true if and only if the negation of the material implication from to is true. This is more naturally stated as that the material nonimplication from to is true only if is true and is false.
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, Boolean functions, and propositional calculus—which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables. In particular, truth tables can be used to show whether a propositional expression is true for all legitimate input values, that is, logically valid.
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values true and false, usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses logical operators such as conjunction (and) denoted as ∧, disjunction (or) denoted as ∨, and negation (not) denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction, and division. Boolean algebra is therefore a formal way of describing logical operations in the same way that elementary algebra describes numerical operations.









