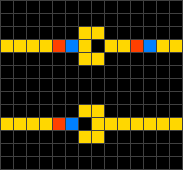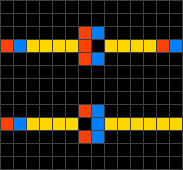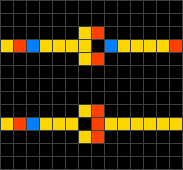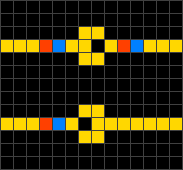The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.

A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.
In automata theory, sequential logic is a type of logic circuit whose output depends not only on the present value of its input signals but on the sequence of past inputs, the input history as well. This is in contrast to combinational logic, whose output is a function of only the present input. That is, sequential logic has state (memory) while combinational logic does not.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science. The word automata comes from the Greek word αὐτόματα, which means "self-making". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite State Machine (FSM).
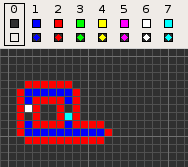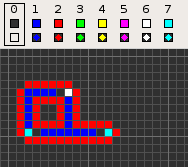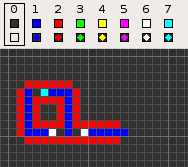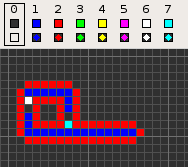
Codd's cellular automaton is a cellular automaton (CA) devised by the British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29. Codd showed that it was possible to make a self-reproducing machine in his CA, in a similar way to von Neumann's universal constructor, but never gave a complete implementation.
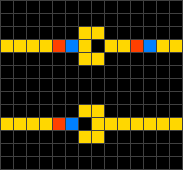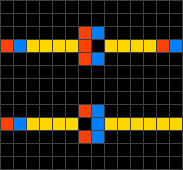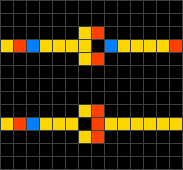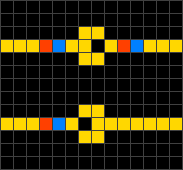
Wireworld is a first proposed by Brian Silverman in 1987, as part of his program Phantom Fish Tank. It subsequently became more widely known as a result of an article in the "Computer Recreations" column of Scientific American. Wireworld is particularly suited to simulating transistors, and Wireworld is Turing-complete.

Von Neumann cellular automata are the original expression of cellular automata, the development of which was prompted by suggestions made to John von Neumann by his close friend and fellow mathematician Stanislaw Ulam. Their original purpose was to provide insight into the logical requirements for machine self-replication, and they were used in von Neumann's universal constructor.

A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.

A cyclic cellular automaton is a kind of cellular automaton rule developed by David Griffeath and studied by several other cellular automaton researchers. In this system, each cell remains unchanged until some neighboring cell has a modular value exactly one unit larger than that of the cell itself, at which point it copies its neighbor's value. One-dimensional cyclic cellular automata can be interpreted as systems of interacting particles, while cyclic cellular automata in higher dimensions exhibit complex spiraling behavior.

A billiard-ball computer, a type of conservative logic circuit, is an idealized model of a reversible mechanical computer based on Newtonian dynamics, proposed in 1982 by Edward Fredkin and Tommaso Toffoli. Instead of using electronic signals like a conventional computer, it relies on the motion of spherical billiard balls in a friction-free environment made of buffers against which the balls bounce perfectly. It was devised to investigate the relation between computation and reversible processes in physics.

Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm", which will become the daughter loop. The "genes" instruct it to make three left turns, completing the loop, which then disconnects from its parent.
The idea of human artifacts being given life has fascinated humankind for at least 3000 years. As seen in tales ranging from Pygmalion to Frankenstein, humanity has long been intrigued by the concept of artificial life.
Quantum dot cellular automata are a proposed improvement on conventional computer design (CMOS), which have been devised in analogy to conventional models of cellular automata introduced by John von Neumann.

John von Neumann's universal constructor is a self-replicating machine in a cellular automata (CA) environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in 1966 by Arthur W. Burks after von Neumann's death. While typically not as well known as von Neumann's other work, it is regarded as foundational for automata theory, complex systems, and artificial life. Indeed, Nobel Laureate Sydney Brenner considered Von Neumann's work on self-reproducing automata central to biological theory as well, allowing us to "discipline our thoughts about machines, both natural and artificial."
A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.

In the mathematical study of cellular automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.

The Byl's loop is an artificial lifeform similar in concept to Langton's loop. It is a two-dimensional, 5-neighbor cellular automaton with 6 states per cell, and was developed in 1989 by John Byl, from the Department of Mathematical Sciences of Trinity Western University.

A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.

CoDi is a cellular automaton (CA) model for spiking neural networks (SNNs). CoDi is an acronym for Collect and Distribute, referring to the signals and spikes in a neural network.

The Ulam–Warburton cellular automaton (UWCA) is a 2-dimensional fractal pattern that grows on a regular grid of cells consisting of squares. Starting with one square initially ON and all others OFF, successive iterations are generated by turning ON all squares that share precisely one edge with an ON square. This is the von Neumann neighborhood. The automaton is named after the Polish-American mathematician and scientist Stanislaw Ulam and the Scottish engineer, inventor and amateur mathematician Mike Warburton.