 | This article includes a list of general references, but it lacks sufficient corresponding inline citations .(June 2023) |
 | This article relies largely or entirely on a single source .(April 2024) |
In mathematics, the phrase "of the form" indicates that a mathematical object, or (more frequently) a collection of objects, follows a certain pattern of expression. It is frequently used to reduce the formality of mathematical proofs.
Here is a proof which should be appreciable with limited mathematical background:
Statement:
The product of any two even natural numbers is also even.
Proof:
Any even natural number is of the form 2n, where n is a natural number. Therefore, let us assume that we have two even numbers which we will denote by 2k and 2l. Their product is (2k)(2l) = 4(kl) = 2(2kl). Since 2kl is also a natural number, the product is even.
Note:
In this case, both exhaustivity and exclusivity were needed. That is, it was not only necessary that every even number is of the form 2n (exhaustivity), but also that every expression of the form 2n is an even number (exclusivity). This will not be the case in every proof, but normally, at least exhaustivity is implied by the phrase of the form.
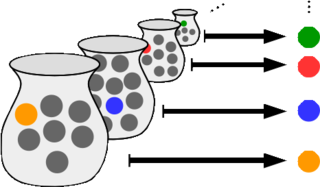
In mathematics, the axiom of choice, abbreviated AC or AoC, is an axiom of set theory equivalent to the statement that a Cartesian product of a collection of non-empty sets is non-empty. Informally put, the axiom of choice says that given any collection of sets, each containing at least one element, it is possible to construct a new set by choosing one element from each set, even if the collection is infinite. Formally, it states that for every indexed family of nonempty sets, there exists an indexed set such that for every . The axiom of choice was formulated in 1904 by Ernst Zermelo in order to formalize his proof of the well-ordering theorem.
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers. Equivalently, a set is countable if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements.
Mathematical induction is a method for proving that a statement is true for every natural number , that is, that the infinitely many cases all hold. This is done by first proving a simple case, then also showing that if we assume the claim is true for a given case, then the next case is also true. Informal metaphors help to explain this technique, such as falling dominoes or climbing a ladder:
Mathematical induction proves that we can climb as high as we like on a ladder, by proving that we can climb onto the bottom rung and that from each rung we can climb up to the next one.
In the philosophy of mathematics, constructivism asserts that it is necessary to find a specific example of a mathematical object in order to prove that an example exists. Contrastingly, in classical mathematics, one can prove the existence of a mathematical object without "finding" that object explicitly, by assuming its non-existence and then deriving a contradiction from that assumption. Such a proof by contradiction might be called non-constructive, and a constructivist might reject it. The constructive viewpoint involves a verificational interpretation of the existential quantifier, which is at odds with its classical interpretation.
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
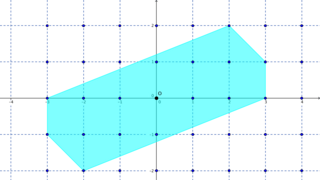
In mathematics, Minkowski's theorem is the statement that every convex set in which is symmetric with respect to the origin and which has volume greater than contains a non-zero integer point. The theorem was proved by Hermann Minkowski in 1889 and became the foundation of the branch of number theory called the geometry of numbers. It can be extended from the integers to any lattice and to any symmetric convex set with volume greater than , where denotes the covolume of the lattice.
A mathematical proof is a deductive argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in all possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work.
In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n × n orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact.
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan.
In mathematics, Bertrand's postulate states that for each there is a prime such that . First conjectured in 1845 by Joseph Bertrand, it was first proven by Chebyshev, and a shorter but also advanced proof was given by Ramanujan.
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set. In this technique, which van Lint & Wilson (2001) call "one of the most important tools in combinatorics", one describes a finite set from two perspectives leading to two distinct expressions for the size of the set. Since both expressions equal the size of the same set, they equal each other.
In Euclidean geometry, a regular polygon is a polygon that is direct equiangular and equilateral. Regular polygons may be either convex, star or skew. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof, which proves the existence of a particular kind of object without providing an example. For avoiding confusion with the stronger concept that follows, such a constructive proof is sometimes called an effective proof.
In mathematics, the double factorial of a number n, denoted by n‼, is the product of all the positive integers up to n that have the same parity as n. That is,
In mathematics, the term combinatorial proof is often used to mean either of two types of mathematical proof:
The language of mathematics has a vast vocabulary of specialist and technical terms. It also has a certain amount of jargon: commonly used phrases which are part of the culture of mathematics, rather than of the subject. Jargon often appears in lectures, and sometimes in print, as informal shorthand for rigorous arguments or precise ideas. Much of this is common English, but with a specific non-obvious meaning when used in a mathematical sense.
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. It was first proven by Euclid in his work Elements. There are several proofs of the theorem.
Boolean algebra is a mathematically rich branch of abstract algebra. Stanford Encyclopaedia of Philosophy defines Boolean algebra as 'the algebra of two-valued logic with only sentential connectives, or equivalently of algebras of sets under union and complementation.' Just as group theory deals with groups, and linear algebra with vector spaces, Boolean algebras are models of the equational theory of the two values 0 and 1. Common to Boolean algebras, groups, and vector spaces is the notion of an algebraic structure, a set closed under some operations satisfying certain equations.
In mathematics, the irrational numbers are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being incommensurable, meaning that they share no "measure" in common, that is, there is no length, no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself.
 | This mathematics-related article is a stub. You can help Wikipedia by expanding it. |