On (the) Sizes and Distances (of the Sun and Moon) may refer to:
 | This disambiguation page lists articles associated with the title On Sizes and Distances. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
The astronomical unit is a unit of length, roughly the distance from Earth to the Sun and equal to about 150 million kilometres. The actual distance varies as Earth orbits the Sun, from a maximum (aphelion) to a minimum (perihelion) and back again once each year. The AU was originally conceived as the average of Earth's aphelion and perihelion; however, since 2012 it has been defined as exactly 149597870700 m.
Hipparchus of Nicaea was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry but is most famous for his incidental discovery of precession of the equinoxes.
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. Due to foreshortening, nearby objects show a larger parallax than farther objects when observed from different positions, so parallax can be used to determine distances.
Year 129 BC was a year of the pre-Julian Roman calendar. At the time it was known as the Year of the Consulship of Tuditanus and Aquillius and the Sixth Year of Yuanguang. The denomination 129 BC for this year has been used since the early medieval period, when the Anno Domini calendar era became the prevalent method in Europe for naming years.
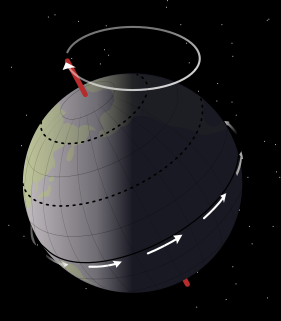
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In particular, it can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 25,772 years. This is similar to the precession of a spinning-top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—nutation and polar motion—are much smaller in magnitude.
Aristarchus of Samos was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the known universe with the Earth revolving around it. He was influenced by Philolaus of Croton, but Aristarchus identified the "central fire" with the Sun, and he put the other planets in their correct order of distance around the Sun. Like Anaxagoras before him, he suspected that the stars were just other bodies like the Sun, albeit farther away from Earth. His astronomical ideas were often rejected in favor of the geocentric theories of Aristotle and Ptolemy. Nicolaus Copernicus attributed the heliocentric theory to Aristarchus.
Timocharis of Alexandria was a Greek astronomer and philosopher. Likely born in Alexandria, he was a contemporary of Euclid.
Heliocentrism is the astronomical model in which the Earth and planets revolve around the Sun at the center of the Universe. Historically, heliocentrism was opposed to geocentrism, which placed the Earth at the center. The notion that the Earth revolves around the Sun had been proposed as early as the 3rd century BC by Aristarchus of Samos, but at least in the medieval world, Aristarchus' heliocentrism attracted little attention—possibly because of the loss of scientific works of the Hellenistic period.
Lunar distance, also called Earth–Moon distance, Earth–Moon characteristic distance, or distance to the Moon, is a unit of measure in astronomy. It is the average distance from the center of Earth to the center of the Moon. More technically, it is the mean semi-major axis of the geocentric lunar orbit. It may also refer to the time-averaged distance between the centers of the Earth and the Moon, or less commonly, the instantaneous Earth–Moon distance. The lunar distance is approximately 400,000 km, or a quarter of a million miles.
Seleucus of Seleucia was a Hellenistic astronomer and philosopher. Coming from Seleucia on the Tigris, Mesopotamia, the capital of the Seleucid Empire, or, alternatively, Seleukia on the Erythraean Sea, he is best known as a proponent of heliocentrism and for his theory of the origin of tides.
A degree, usually denoted by °, is a measurement of a plane angle in which one full rotation is 360 degrees.
On the Sizes and Distances is widely accepted as the only extant work written by Aristarchus of Samos, an ancient Greek astronomer who lived circa 310–230 BCE. This work calculates the sizes of the Sun and Moon, as well as their distances from the Earth in terms of Earth's radius.
On Sizes and Distances is a text by the ancient Greek astronomer Hipparchus in which approximations are made for the radii of the Sun and the Moon as well as their distances from the Earth. It is not extant, but some of its contents have been preserved in the works of Ptolemy and his commentator Pappus of Alexandria. Several modern historians have attempted to reconstruct the methods of Hipparchus using the available texts.
Babylonian mathematics was any mathematics developed or practiced by the people of Mesopotamia, from the days of the early Sumerians to the centuries following the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited. In respect of time they fall in two distinct groups: one from the Old Babylonian period, the other mainly Seleucid from the last three or four centuries BC. In respect of content, there is scarcely any difference between the two groups of texts. Babylonian mathematics remained constant, in character and content, for nearly two millennia.
Aristarchus may refer to:
Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the language of scholarship throughout the Hellenistic world following the conquests of Alexander. This phase of Greek astronomy is also known as Hellenistic astronomy, while the pre-Hellenistic phase is known as Classical Greek astronomy. During the Hellenistic and Roman periods, much of the Greek and non-Greek astronomers working in the Greek tradition studied at the Musaeum and the Library of Alexandria in Ptolemaic Egypt.
Trigonometry is a branch of mathematics that studies the relationships between the sides and the angles in triangles. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves.
Early study of triangles can be traced to the 2nd millennium BC, in Egyptian mathematics and Babylonian mathematics. Trigonometry was also prevalent in Kushite mathematics. Systematic study of trigonometric functions began in Hellenistic mathematics, reaching India as part of Hellenistic astronomy. In Indian astronomy, the study of trigonometric functions flourished in the Gupta period, especially due to Aryabhata, who discovered the sine function. During the Middle Ages, the study of trigonometry continued in Islamic mathematics, by mathematicians such as Al-Khwarizmi and Abu al-Wafa. It became an independent discipline in the Islamic world, where all six trigonometric functions were known. Translations of Arabic and Greek texts led to trigonometry being adopted as a subject in the Latin West beginning in the Renaissance with Regiomontanus. The development of modern trigonometry shifted during the western Age of Enlightenment, beginning with 17th-century mathematics and reaching its modern form with Leonhard Euler (1748).
This is a timeline of ancient Greek mathematicians.