Related Research Articles

In probability theory and statistics, the binomial distribution with parameters n and p is the discrete probability distribution of the number of successes in a sequence of n independent experiments, each asking a yes–no question, and each with its own Boolean-valued outcome: success or failure. A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance.

In mathematics, the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 and some from 1 and 2. Starting from 0 and 1, the sequence begins

In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.

Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples of oscillation include a swinging pendulum and alternating current. Oscillations can be used in physics to approximate complex interactions, such as those between atoms.

The tiger is a large cat and a member of the genus Panthera native to Asia. It has a powerful, muscular body with a large head and paws, a long tail and orange fur with black, mostly vertical stripes. It is traditionally classified into nine recent subspecies, though some recognise only two subspecies, mainland Asian tigers and the island tigers of the Sunda Islands.

In mathematics, a divisor of an integer also called a factor of is an integer that may be multiplied by some integer to produce In this case, one also says that is a multiple of An integer is divisible or evenly divisible by another integer if is a divisor of ; this implies dividing by leaves no remainder.

The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form:
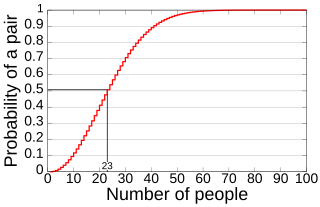
In probability theory, the birthday problem asks for the probability that, in a set of n randomly chosen people, at least two will share the same birthday. The birthday paradox refers to the counterintuitive fact that only 23 people are needed for that probability to exceed 50%.

The speed of sound is the distance travelled per unit of time by a sound wave as it propagates through an elastic medium. More simply, the speed of sound is how fast vibrations travel. At 20 °C (68 °F), the speed of sound in air, is about 343 m/s, or 1 km in 2.91 s or one mile in 4.69 s. It depends strongly on temperature as well as the medium through which a sound wave is propagating.

The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relative to a rotational axis. It is the ratio between the torque applied and the resulting angular acceleration about that axis. It plays the same role in rotational motion as mass does in linear motion. A body's moment of inertia about a particular axis depends both on the mass and its distribution relative to the axis, increasing with mass & distance from the axis.
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics.
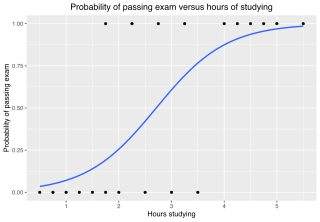
In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression estimates the parameters of a logistic model. In binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
In mathematics, summation is the addition of a sequence of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined.

In biochemistry, Michaelis–Menten kinetics, named after Leonor Michaelis and Maud Menten, is the simplest case of enzyme kinetics, applied to enzyme-catalysed reactions of one substrate and one product. It takes the form of a differential equation describing the reaction rate to , the concentration of the substrate A. Its formula is given by the Michaelis–Menten equation:
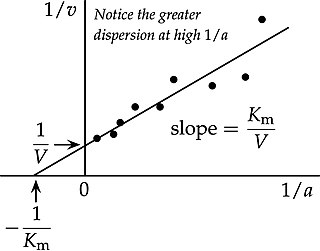
In biochemistry, the Lineweaver–Burk plot is a graphical representation of the Michaelis–Menten equation of enzyme kinetics, described by Hans Lineweaver and Dean Burk in 1934.
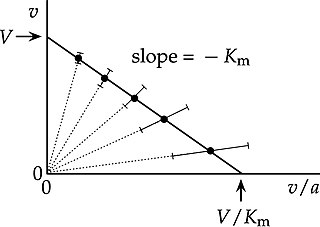
In biochemistry, an Eadie–Hofstee plot is a graphical representation of the Michaelis–Menten equation in enzyme kinetics. It has been known by various different names, including Eadie plot, Hofstee plot and Augustinsson plot. Attribution to Woolf is often omitted, because although Haldane and Stern credited Woolf with the underlying equation, it was just one of the three linear transformations of the Michaelis–Menten equation that they initially introduced. However, Haldane indicated in 1957 that Woolf had indeed found the three linear forms:
In 1932, Dr. Kurt Stern published a German translation of my book Enzymes, with numerous additions to the English text. On pp. 119–120, I described some graphical methods, stating that they were due to my friend Dr. Barnett Woolf. [...] Woolf pointed out that linear graphs are obtained when is plotted against , against , or against , the first plot being most convenient unless inhibition is being studied.
The surface gravity, g, of an astronomical object is the gravitational acceleration experienced at its surface at the equator, including the effects of rotation. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in order not to disturb the system, has negligible mass. For objects where the surface is deep in the atmosphere and the radius not known, the surface gravity is given at the 1 bar pressure level in the atmosphere.

In biochemistry, a Hanes–Woolf plot, Hanes plot, or plot of against is a graphical representation of enzyme kinetics in which the ratio of the initial substrate concentration to the reaction velocity is plotted against . It is based on the rearrangement of the Michaelis–Menten equation shown below: