In mathematics, the Weil conjectures were some highly influential proposals by André Weil (1949), which led to a successful multi-decade program to prove them, in which many leading researchers developed the framework of modern algebraic geometry and number theory.
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F, or equivalently, a one-dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group. The importance of the concept, however, stems from its application to representations of Lie algebras and hence also to representations of algebraic and Lie groups. In this context, a weight of a representation is a generalization of the notion of an eigenvalue, and the corresponding eigenspace is called a weight space.
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry. In most of these theories, the even elements of the superalgebra correspond to bosons and odd elements to fermions.

In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebras with additional structure. In general, a quantum group is some kind of Hopf algebra. There is no single, all-encompassing definition, but instead a family of broadly similar objects.

In transcendental number theory, the Lindemann–Weierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states the following.
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2 × 2 integer matrices of determinant 1, such that the off-diagonal entries are even. More generally, the notion of congruence subgroup can be defined for arithmetic subgroups of algebraic groups; that is, those for which we have a notion of 'integral structure' and can define reduction maps modulo an integer.
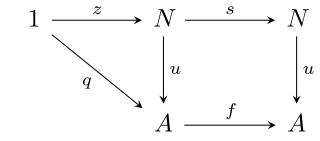
In category theory, a natural number object (NNO) is an object endowed with a recursive structure similar to natural numbers. More precisely, in a category E with a terminal object 1, an NNO N is given by:
- a global element z : 1 → N, and
- an arrow s : N → N,
In mathematics, infinite-dimensional holomorphy is a branch of functional analysis. It is concerned with generalizations of the concept of holomorphic function to functions defined and taking values in complex Banach spaces, typically of infinite dimension. It is one aspect of nonlinear functional analysis.
In theoretical physics and mathematics, a Wess–Zumino–Witten (WZW) model, also called a Wess–Zumino–Novikov–Witten model, is a type of two-dimensional conformal field theory named after Julius Wess, Bruno Zumino, Sergei Novikov and Edward Witten. The symmetry algebra of a WZW model is an affine Lie algebra.
In mathematics, Lie algebra cohomology is a cohomology theory for Lie algebras. It was first introduced in 1929 by Élie Cartan to study the topology of Lie groups and homogeneous spaces by relating cohomological methods of Georges de Rham to properties of the Lie algebra. It was later extended by Claude Chevalley and Samuel Eilenberg (1948) to coefficients in an arbitrary Lie module.
In algebraic geometry, local cohomology is an analog of relative cohomology. Alexander Grothendieck introduced it in seminars in Harvard in 1961 written up by Hartshorne (1967), and in 1961-2 at IHES written up as SGA2 - Grothendieck (1968), republished as Grothendieck (2005).
In mathematics, specifically in operator K-theory, the Baum–Connes conjecture suggests a link between the K-theory of the reduced C*-algebra of a group and the K-homology of the classifying space of proper actions of that group. The conjecture sets up a correspondence between different areas of mathematics, with the K-homology of the classifying space being related to geometry, differential operator theory, and homotopy theory, while the K-theory of the group's reduced C*-algebra is a purely analytical object.
In mathematics, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra acting on a Hilbert space in the presence of a trace. The first such result was proved by F.J. Murray and John von Neumann in the 1930s and applies to the von Neumann algebra generated by a discrete group or by the dynamical system associated with a measurable transformation preserving a probability measure. Another important application is in the theory of unitary representations of unimodular locally compact groups, where the theory has been applied to the regular representation and other closely related representations. In particular this framework led to an abstract version of the Plancherel theorem for unimodular locally compact groups due to Irving Segal and Forrest Stinespring and an abstract Plancherel theorem for spherical functions associated with a Gelfand pair due to Roger Godement. Their work was put in final form in the 1950s by Jacques Dixmier as part of the theory of Hilbert algebras. It was not until the late 1960s, prompted partly by results in algebraic quantum field theory and quantum statistical mechanics due to the school of Rudolf Haag, that the more general non-tracial Tomita–Takesaki theory was developed, heralding a new era in the theory of von Neumann algebras.
In mathematics, Hahn series are a type of formal infinite series. They are a generalization of Puiseux series and were first introduced by Hans Hahn in 1907. They allow for arbitrary exponents of the indeterminate so long as the set supporting them forms a well-ordered subset of the value group. Hahn series were first introduced, as groups, in the course of the proof of the Hahn embedding theorem and then studied by him as fields in his approach to Hilbert's seventeenth problem.
This is a glossary for the terminology applied in the mathematical theories of Lie algebras. The statements in this glossary mainly focus on the algebraic sides of the concepts, without referring to Lie groups or other related subjects.
In mathematics, Kadison transitivity theorem is a result in the theory of C*-algebras that, in effect, asserts the equivalence of the notions of topological irreducibility and algebraic irreducibility of representations of C*-algebras. It implies that, for irreducible representations of C*-algebras, the only non-zero linear invariant subspace is the whole space.

In the theory of Lie groups, the exponential map is a map from the Lie algebra of a Lie group to the group, which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary reasons that Lie algebras are a useful tool for studying Lie groups.
In the theory of C*-algebras, the universal representation of a C*-algebra is a faithful representation which is the direct sum of the GNS representations corresponding to the states of the C*-algebra. The various properties of the universal representation are used to obtain information about the ideals and quotients of the C*-algebra. The close relationship between an arbitrary representation of a C*-algebra and its universal representation can be exploited to obtain several criteria for determining whether a linear functional on the algebra is ultraweakly continuous. The method of using the properties of the universal representation as a tool to prove results about the C*-algebra and its representations is commonly referred to as universal representation techniques in the literature.
In mathematics, the Kadison–Singer problem, posed in 1959, was a problem in functional analysis about whether certain extensions of certain linear functionals on certain C*-algebras were unique. The uniqueness was proven in 2013.

In computing, a Digital Object Identifier or DOI is a persistent identifier or handle used to identify objects uniquely, standardized by the International Organization for Standardization (ISO). An implementation of the Handle System, DOIs are in wide use mainly to identify academic, professional, and government information, such as journal articles, research reports and data sets, and official publications though they also have been used to identify other types of information resources, such as commercial videos.
Mathematical Reviews is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science. The AMS also publishes an associated online bibliographic database called MathSciNet which contains an electronic version of Mathematical Reviews and additionally contains citation information for over 3.5 million items as of 2018.

Richard V. Kadison was an American mathematician known for his contributions to the study of operator algebras.













