This page is based on this
Wikipedia article Text is available under the
CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and Hans Hahn. This grew eventually into the Artin–Schreier theory of ordered fields and formally real fields.

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The word "partial" in the names "partial order" or "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.

Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node and explores as far as possible along each branch before backtracking.
This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by edges.
In mathematics, a monoidal category is a category C equipped with a bifunctor
The category Ord has preordered sets as objects and order-preserving functions as morphisms. This is a category because the composition of two order-preserving functions is order preserving and the identity map is order preserving.
In topology, an Alexandrov topology is a topology in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open; in Alexandrov topologies the finite restriction is dropped.
In the branch of mathematics known as topology, the specialization (or canonical) preorder is a natural preorder on the set of the points of a topological space. For most spaces that are considered in practice, namely for all those that satisfy the T0 separation axiom, this preorder is even a partial order (called the specialization order). On the other hand, for T1 spaces the order becomes trivial and is of little interest.

In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set, some of whose members may be tied with each other. Weak orders are a generalization of totally ordered sets and are in turn generalized by partially ordered sets and preorders.
In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic. Interior algebras form a variety of modal algebras.
In mathematics a field of sets is a pair
where
is a set and
is an algebra over
i.e., a non-empty subset of the power set of
closed under the intersection and union of pairs of sets and under complements of individual sets. In other words,
forms a subalgebra of the power set Boolean algebra of
. Elements of
are called points and those of
are called complexes and are said to be the admissible sets of
.
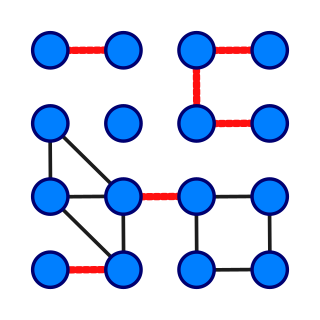
In graph theory, a bridge, isthmus, cut-edge, or cut arc is an edge of a graph whose deletion increases its number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle. A graph is said to be bridgeless or isthmus-free if it contains no bridges.

In mathematics, an ordered vector space or partially ordered vector space is a vector space equipped with a partial order that is compatible with the vector space operations.
In graph theory, the strongly connected components of a directed graph may be found using an algorithm that uses depth-first search in combination with two stacks, one to keep track of the vertices in the current component and the second to keep track of the current search path. Versions of this algorithm have been proposed by Purdom (1970), Munro (1971), Dijkstra (1976), Cheriyan & Mehlhorn (1996), and Gabow (2000); of these, Dijkstra's version was the first to achieve linear time.
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points.
In mathematics, a preordered class is a class equipped with a preorder.
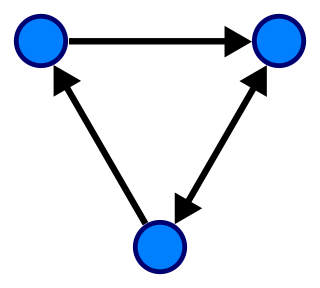
In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by edges, where the edges have a direction associated with them.
In graph theory, a bipolar orientation or st-orientation of an undirected graph is an assignment of a direction to each edge that causes the graph to become a directed acyclic graph with a single source s and a single sink t, and an st-numbering of the graph is a topological ordering of the resulting directed acyclic graph.





