
In mathematical physics, the Dirac delta distribution, also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one.
In probability theory, the central limit theorem (CLT) establishes that, in many situations, for independent and identically distributed random variables, the sampling distribution of the standardized sample mean tends towards the standard normal distribution even if the original variables themselves are not normally distributed.

In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown. It is one of the best known Lévy processes and occurs frequently in pure and applied mathematics, economics, quantitative finance, evolutionary biology, and physics.
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant. It is named after the Russian mathematician Andrey Markov, although it appeared earlier in the work of Pafnuty Chebyshev, and many sources, especially in analysis, refer to it as Chebyshev's inequality or Bienaymé's inequality.

Electrostatics is a branch of physics that studies electric charges at rest.
In mathematics, the Fourier inversion theorem says that for many types of functions it is possible to recover a function from its Fourier transform. Intuitively it may be viewed as the statement that if we know all frequency and phase information about a wave then we may reconstruct the original wave precisely.
In probability theory, a Chernoff bound is an exponentially decreasing upper bound on the tail of a random variable based on its moment generating function. The minimum of all such exponential bounds forms the Chernoff or Chernoff-Cramér bound, which may decay faster than exponential. It is especially useful for sums of independent random variables, such as sums of Bernoulli random variables.
In mathematics, more specifically in mathematical analysis, the Cauchy product is the discrete convolution of two infinite series. It is named after the French mathematician Augustin-Louis Cauchy.
In probability theory, Hoeffding's inequality provides an upper bound on the probability that the sum of bounded independent random variables deviates from its expected value by more than a certain amount. Hoeffding's inequality was proven by Wassily Hoeffding in 1963.
In information theory, Shannon's source coding theorem establishes the limits to possible data compression, and the operational meaning of the Shannon entropy.
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence defines a series S that is denoted

Arc length is the distance between two points along a section of a curve.
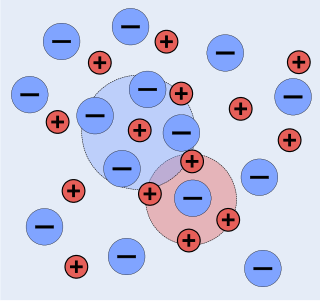
The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activities of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.
In mathematics and economics, transportation theory or transport theory is a name given to the study of optimal transportation and allocation of resources. The problem was formalized by the French mathematician Gaspard Monge in 1781.
Equilibrium constants are determined in order to quantify chemical equilibria. When an equilibrium constant K is expressed as a concentration quotient,
The Price of Anarchy (PoA) is a concept in economics and game theory that measures how the efficiency of a system degrades due to selfish behavior of its agents. It is a general notion that can be extended to diverse systems and notions of efficiency. For example, consider the system of transportation of a city and many agents trying to go from some initial location to a destination. Let efficiency in this case mean the average time for an agent to reach the destination. In the 'centralized' solution, a central authority can tell each agent which path to take in order to minimize the average travel time. In the 'decentralized' version, each agent chooses its own path. The Price of Anarchy measures the ratio between average travel time in the two cases.
Congestion games are a class of games in game theory first proposed by American economist Robert W. Rosenthal in 1973. In a congestion game the payoff of each player depends on the resources it chooses and the number of players choosing the same resource. Congestion games are a special case of potential games. Rosenthal proved that any congestion game is a potential game and Monderer and Shapley (1996) proved the converse: for any potential game, there is a congestion game with the same potential function.
In probability theory, concentration inequalities provide bounds on how a random variable deviates from some value. The law of large numbers of classical probability theory states that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean. Recent results show that such behavior is shared by other functions of independent random variables.
In mathematics, a smooth maximum of an indexed family x1, ..., xn of numbers is a smooth approximation to the maximum function meaning a parametric family of functions such that for every α, the function is smooth, and the family converges to the maximum function as . The concept of smooth minimum is similarly defined. In many cases, a single family approximates both: maximum as the parameter goes to positive infinity, minimum as the parameter goes to negative infinity; in symbols, as and as . The term can also be used loosely for a specific smooth function that behaves similarly to a maximum, without necessarily being part of a parametrized family.

The Price of Anarchy (PoA) is a concept in game theory and mechanism design that measures how the social welfare of a system degrades due to selfish behavior of its agents. It has been studied extensively in various contexts, particularly in auctions.














































