In control theory, a proper transfer function is a transfer function in which the degree of the numerator does not exceed the degree of the denominator. A strictly proper transfer function is a transfer function where the degree of the numerator is less than the degree of the denominator.
Control theory in control systems engineering is a subfield of mathematics that deals with the control of continuously operating dynamical systems in engineered processes and machines. The objective is to develop a control model for controlling such systems using a control action in an optimum manner without delay or overshoot and ensuring control stability.
In engineering, a transfer function of an electronic or control system component is a mathematical function which theoretically models the device's output for each possible input. In its simplest form, this function is a two-dimensional graph of an independent scalar input versus the dependent scalar output, called a transfer curve or characteristic curve. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory.
The degree of a polynomial is the highest degree of its monomials with non-zero coefficients. The degree of a term is the sum of the exponents of the variables that appear in it, and thus is a non-negative integer. The term order has been used as a synonym of degree but, nowadays, may refer to several other concepts . For example, the polynomial which can also be expressed as has three terms. The first term has a degree of 5, the second term has a degree of 1, and the last term has a degree of 0. Therefore, the polynomial has a degree of 5, which is the highest degree of any term.
The difference between the degree of the denominator (number of poles) and degree of the numerator (number of zeros) is the relative degree of the transfer function.
The following transfer function:
is proper, because
is biproper, because
but is not strictly proper, because
The following transfer function is not proper (or strictly proper)
because
The following transfer function is strictly proper
because
A proper transfer function will never grow unbounded as the frequency approaches infinity:
A strictly proper transfer function will approach zero as the frequency approaches infinity (which is true for all physical processes):
Also, the integral of the real part of a strictly proper transfer function is zero.
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.
In mathematics, and more specifically in calculus, L'Hôpital's rule or L'Hospital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to an expression that can be evaluated by substitution, allowing easier evaluation of the limit. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the contribution of the rule is often attributed to L'Hôpital, the theorem was first introduced to L'Hôpital in 1694 by the Swiss mathematician Johann Bernoulli.
In the mathematical subfield of numerical analysis, a B-spline, or basis spline, is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. Any spline function of given degree can be expressed as a linear combination of B-splines of that degree. Cardinal B-splines have knots that are equidistant from each other. B-splines can be used for curve-fitting and numerical differentiation of experimental data.
In mathematics, a transcendental number is a real number or complex number that is not an algebraic number—that is, not a root of a nonzero polynomial equation with integer coefficients. The best-known transcendental numbers are π and e.
In mathematics, a zero of a function f(x) is a value a such that f(a) = 0.
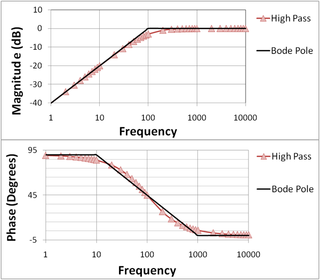
In electrical engineering and control theory, a Bode plot is a graph of the frequency response of a system. It is usually a combination of a Bode magnitude plot, expressing the magnitude of the frequency response, and a Bode phase plot, expressing the phase shift.
In algebra, the partial fraction decomposition or partial fraction expansion of a rational function is an operation that consists of expressing the fraction as a sum of a polynomial and one or several fractions with a simpler denominator.
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input.
In mathematics, a rational function is any function which can be defined by a rational fraction, i.e. an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rational numbers; they may be taken in any field K. In this case, one speaks of a rational function and a rational fraction over K. The values of the variables may be taken in any field L containing K. Then the domain of the function is the set of the values of the variables for which the denominator is not zero and the codomain is L.
In calculus and other branches of mathematical analysis, limits involving an algebraic combination of functions in an independent variable may often be evaluated by replacing these functions by their limits; if the expression obtained after this substitution does not give enough information to determine the original limit, it is said to take on an indeterminate form. The term was originally introduced by Cauchy's student Moigno in the middle of the 19th century.
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables whose values evolve through time in a way that depends on the values they have at any given time and also depends on the externally imposed values of input variables. Output variables’ values depend on the values of the state variables.
In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary complex values.
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A common, vulgar, or simple fraction consists of an integer numerator displayed above a line, and a non-zero integer denominator, displayed below that line. Numerators and denominators are also used in fractions that are not common, including compound fractions, complex fractions, and mixed numerals.
In mathematics, signal processing and control theory, a pole–zero plot is a graphical representation of a rational transfer function in the complex plane which helps to convey certain properties of the system such as:
In algebra, an algebraic fraction is a fraction whose numerator and denominator are algebraic expressions. Two examples of algebraic fractions are and . Algebraic fractions are subject to the same laws as arithmetic fractions.
In systems theory, a realization of a state space model is an implementation of a given input-output behavior. That is, given an input-output relationship, a realization is a quadruple of (time-varying) matrices such that
A hyperelliptic curve is a class of algebraic curves. Hyperelliptic curves exist for every genus . The general formula of Hyperelliptic curve over a finite field is given by
In probability theory, a 2-EPT probability density function is a class of probability density functions on the real line. The class contains the density functions of all distributions that have characteristic functions that are strictly proper rational functions.
