
A circle is a shape consisting of all points in a plane that are a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U shaped. It fits several other superficially different mathematical descriptions, which can all be proved to define exactly the same curves.

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More precisely, a straight line is said to be a tangent of a curve y = f(x) at a point x = c on the curve if the line passes through the point (c, f ) on the curve and has slope f'(c), where f' is the derivative of f. A similar definition applies to space curves and curves in n-dimensional Euclidean space.
In mathematics, a quadric or quadric surface, is a generalization of conic sections. It is a hypersurface in a (D + 1)-dimensional space, and it is defined as the zero set of an irreducible polynomial of degree two in D + 1 variables. When the defining polynomial is not absolutely irreducible, the zero set is generally not considered a quadric, although it is often called a degenerate quadric or a reducible quadric.
In geometry, a secant of a curve is a line that intersects the curve in at least two (distinct) points. The word secant comes from the Latin word secare, meaning to cut. In the case of a circle, a secant will intersect the circle in exactly two points and a chord is the line segment determined by these two points, that is the interval on a secant whose endpoints are these points.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.
In geometry, a striking feature of projective planes is the symmetry of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this concept. There are two approaches to the subject of duality, one through language and the other a more functional approach through special mappings. These are completely equivalent and either treatment has as its starting point the axiomatic version of the geometries under consideration. In the functional approach there is a map between related geometries that is called a duality. Such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite-dimensional projective geometry.

In geometry, focuses or foci, singular focus, are special points with reference to which any of a variety of curves is constructed. For example, one or two foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola. In addition, two foci are used to define the Cassini oval and the Cartesian oval, and more than two foci are used in defining an n-ellipse.
In mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation. It is generally considered to be the simplest example of a projective variety that is not linear or a hypersurface, and is given as such in most textbooks on algebraic geometry. It is the three-dimensional case of the rational normal curve, and is the image of a Veronese map of degree three on the projective line.
An oval is a closed curve in a plane which "loosely" resembles the outline of an egg. The term is not very specific, but in some areas it is given a more precise definition, which may include either one or two axes of symmetry. In common English, the term is used in a broader sense: any shape which reminds one of an egg. The three-dimensional version of an oval is called an ovoid.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".

In projective geometry an oval is a circle-like pointset (curve) in a plane that is defined by incidence properties. The standard examples are the nondegenerate conics. However, a conic is only defined in a pappian plane, whereas an oval may exist in any type of projective plane. In the literature, there are many criteria which imply that an oval is a conic, but there are many examples, both infinite and finite, of ovals in pappian planes which are not conics.

In projective geometry an ovoid is a sphere like pointset (surface) in a projective space of dimension d ≥ 3. Simple examples in a real projective space are hyperspheres (quadrics). The essential geometric properties of an ovoid are:
- Any line intersects in at most 2 points,
- The tangents at a point cover a hyperplane, and
- contains no lines.
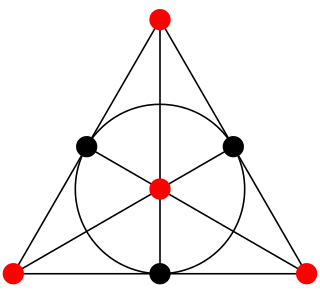
An (simple) arc in finite projective geometry is a set of points which satisfies, in an intuitive way, a feature of curved figures in continuous geometries. Loosely speaking, they are sets of points that are far from "line-like" in a plane or far from "plane-like" in a three-dimensional space. In this finite setting it is typical to include the number of points in the set in the name, so these simple arcs are called k-arcs. An important generalization of the k-arc concept, also referred to as arcs in the literature, are the -arcs.

In mathematics, a conic section is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties.
In Euclidean and projective geometry, just as two (distinct) points determine a line, five points determine a conic. There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.
In mathematics, a quadratic set is a set of points in a projective space that bears the same essential incidence properties as a quadric.

The Steiner conic or more precisely Steiner's generation of a conic, named after the Swiss mathematician Jakob Steiner, is an alternative method to define a non-degenerate projective conic section in a projective plane over a field.
In projective geometry, a von Staudt conic is the point set defined by all the absolute points of a polarity that has absolute points. In the real projective plane a von Staudt conic is a conic section in the usual sense. In more general projective planes this is not always the case. Karl Georg Christian von Staudt introduced this definition in Geometrie der Lage (1847) as part of his attempt to remove all metrical concepts from projective geometry.

In projective geometry Segre's theorem, named after the Italian mathematician Beniamino Segre, is the statement:














