RAPL may refer to:
- L-lysine cyclodeaminase, an enzyme
- Running average power limit, an Intel processor feature
- Right Adjoints Preserve Limits, a theorem regarding adjoint functors in category theory.
RAPL may refer to:
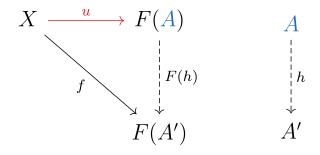
In category theory, a branch of mathematics, a universal property is an important property which is satisfied by a universal morphism. Universal morphisms can also be thought of more abstractly as initial or terminal objects of a comma category. Universal properties occur almost everywhere in mathematics, and hence the precise category theoretic concept helps point out similarities between different branches of mathematics, some of which may even seem unrelated.
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products, pullbacks and inverse limits. The dual notion of a colimit generalizes constructions such as disjoint unions, direct sums, coproducts, pushouts and direct limits.
In mathematics, specifically category theory, adjunction is a relationship that two functors may have. Two functors that stand in this relationship are known as adjoint functors, one being the left adjoint and the other the right adjoint. Pairs of adjoint functors are ubiquitous in mathematics and often arise from constructions of "optimal solutions" to certain problems, such as the construction of a free group on a set in algebra, or the construction of the Stone–Čech compactification of a topological space in topology.
In category theory, a branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X.
In mathematics, particularly linear algebra and functional analysis, a spectral theorem is a result about when a linear operator or matrix can be diagonalized. This is extremely useful because computations involving a diagonalizable matrix can often be reduced to much simpler computations involving the corresponding diagonal matrix. The concept of diagonalization is relatively straightforward for operators on finite-dimensional vector spaces but requires some modification for operators on infinite-dimensional spaces. In general, the spectral theorem identifies a class of linear operators that can be modeled by multiplication operators, which are as simple as one can hope to find. In more abstract language, the spectral theorem is a statement about commutative C*-algebras. See also spectral theory for a historical perspective.

In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix A by producing another matrix, often denoted by AT.
In mathematics, a self-adjoint operator on a finite-dimensional complex vector space V with inner product is a linear map A that is its own adjoint: for all vectors v and w. If V is finite-dimensional with a given orthonormal basis, this is equivalent to the condition that the matrix of A is a Hermitian matrix, i.e., equal to its conjugate transpose A∗. By the finite-dimensional spectral theorem, V has an orthonormal basis such that the matrix of A relative to this basis is a diagonal matrix with entries in the real numbers. In this article, we consider generalizations of this concept to operators on Hilbert spaces of arbitrary dimension.
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous, and the identity function is continuous. The study of Top and of properties of topological spaces using the techniques of category theory is known as categorical topology.
In functional analysis, a branch of mathematics, an operator algebra is an algebra of continuous linear operators on a topological vector space, with the multiplication given by the composition of mappings.
In mathematics, the term adjoint applies in several situations. Several of these share a similar formalism: if A is adjoint to B, then there is typically some formula of the type
In mathematics, specifically in functional analysis, each bounded linear operator on a complex Hilbert space has a corresponding Hermitian adjoint. Adjoints of operators generalize conjugate transposes of square matrices to (possibly) infinite-dimensional situations. If one thinks of operators on a complex Hilbert space as generalized complex numbers, then the adjoint of an operator plays the role of the complex conjugate of a complex number.
In mathematics, particularly category theory, a representable functor is a certain functor from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures allowing one to utilize, as much as possible, knowledge about the category of sets in other settings.
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases.
In category theory, a branch of mathematics, the diagonal functor is given by , which maps objects as well as morphisms. This functor can be employed to give a succinct alternate description of the product of objects within the category : a product is a universal arrow from to . The arrow comprises the projection maps.
X-linked interleukin-1 receptor accessory protein-like 1 is a protein that in humans is encoded by the IL1RAPL1 gene. IL1RAPL1 is composed of 11 exons, about 1.37 Mb total.

In mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms. Like many categories in mathematics, the category of rings is large, meaning that the class of all rings is proper.

X-linked interleukin-1 receptor accessory protein-like 2 is a protein that in humans is encoded by the IL1RAPL2 gene.
In mathematics, a topos is a category that behaves like the category of sheaves of sets on a topological space. Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic.
Rap1 is a small GTPase, which are small cytosolic proteins that act like cellular switches and are vital for effective signal transduction. There are two isoforms of the Rap1 protein, each encoded by a separate gene, RAP1A and RAP1B. Rap1 belongs to Ras-related protein family.