
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer coefficients. For example, the golden ratio, , is an algebraic number, because it is a root of the polynomial x2 − x − 1. That is, it is a value for x for which the polynomial evaluates to zero. As another example, the complex number is algebraic because it is a root of x4 + 4.
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers N = {0, 1, 2, 3, ...}. Equivalently, a set S is countable if there exists an injective function f : S → N from S to N; this means that each element in S may be associated to a unique element in N, or that its elements can be counted one at a time, although the counting may never finish due to an infinite number of elements.

In mathematics, an elliptic curve is a smooth, projective, algebraic curve of genus one, on which there is a specified point O. An elliptic curve is defined over a field K and describes points in K2, the Cartesian product of K with itself. If the field's characteristic is different from 2 and 3, then the curve can be described as a plane algebraic curve which, after a linear change of variables, consists of solutions (x, y) for:

An integer is the number zero (0), a positive natural number or a negative integer with a minus sign. The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface Z or blackboard bold .

Number theory is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers or defined as generalizations of the integers.

Division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication.

In mathematics, a dyadic rational or binary rational is a number that can be expressed as a fraction whose denominator is a power of two. For example, 1/2, 3/2, and 3/8 are dyadic rationals, but 1/3 is not. These numbers are important in computer science because they are the only ones with finite binary representations. Dyadic rationals also have applications in weights and measures, musical time signatures, and early mathematics education. They can accurately approximate any real number.
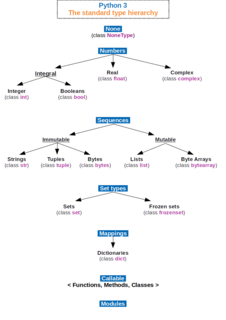
In computer science and computer programming, a data type is a set of possible values and a set of allowed operations on it. A data type tells the compiler or interpreter how the programmer intends to use the data. Most programming languages support basic data types of integer numbers, floating-point numbers, characters and Booleans. A data type constrains the possible values that an expression, such as a variable or a function, might take. This data type defines the operations that can be done on the data, the meaning of the data, and the way values of that type can be stored.

Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern, and pronounced as "b (raised) to the n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:
In calculus, the power rule is used to differentiate functions of the form , whenever is a real number. Since differentiation is a linear operation on the space of differentiable functions, polynomials can also be differentiated using this rule. The power rule underlies the Taylor series as it relates a power series with a function's derivatives.

In mathematics, division by zero is division where the divisor (denominator) is zero. Such a division can be formally expressed as , where a is the dividend (numerator). In ordinary arithmetic, the expression has no meaning, as there is no number that, when multiplied by 0, gives a ; thus, division by zero is undefined. Since any number multiplied by zero is zero, the expression is also undefined; when it is the form of a limit, it is an indeterminate form. Historically, one of the earliest recorded references to the mathematical impossibility of assigning a value to is contained in Anglo-Irish philosopher George Berkeley's criticism of infinitesimal calculus in 1734 in The Analyst.
In mathematics, the term quadratic describes something that pertains to squares, to the operation of squaring, to terms of the second degree, or equations or formulas that involve such terms. Quadratus is Latin for square.
Boundedness or bounded may refer to:
Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, and/or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.

In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q. For example, −3/7 is a rational number, as is every integer. The set of all rational numbers, also referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by boldface Q, or blackboard bold
Some programming languages provide a built-in (primitive) rational data type to represent rational numbers like 1/3 and -11/17 without rounding, and to do arithmetic on them. Examples are the ratio type of Common Lisp, and analogous types provided by most languages for algebraic computation, such as Mathematica and Maple. Many languages that do not have a built-in rational type still provide it as a library-defined type.
In mathematics, statistics and elsewhere, sums of squares occur in a number of contexts:









