Linear filters process time-varying input signals to produce output signals, subject to the constraint of linearity. In most cases these linear filters are also time invariant in which case they can be analyzed exactly using LTI system theory revealing their transfer functions in the frequency domain and their impulse responses in the time domain. Real-time implementations of such linear signal processing filters in the time domain are inevitably causal, an additional constraint on their transfer functions. An analog electronic circuit consisting only of linear components will necessarily fall in this category, as will comparable mechanical systems or digital signal processing systems containing only linear elements. Since linear time-invariant filters can be completely characterized by their response to sinusoids of different frequencies, they are sometimes known as frequency filters.
In engineering, a transfer function of a system, sub-system, or component is a mathematical function that models the system's output for each possible input. It is widely used in electronic engineering tools like circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph of an independent scalar input versus the dependent scalar output. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory.
In telecommunication, a convolutional code is a type of error-correcting code that generates parity symbols via the sliding application of a boolean polynomial function to a data stream. The sliding application represents the 'convolution' of the encoder over the data, which gives rise to the term 'convolutional coding'. The sliding nature of the convolutional codes facilitates trellis decoding using a time-invariant trellis. Time invariant trellis decoding allows convolutional codes to be maximum-likelihood soft-decision decoded with reasonable complexity.

In signal processing, a digital filter is a system that performs mathematical operations on a sampled, discrete-time signal to reduce or enhance certain aspects of that signal. This is in contrast to the other major type of electronic filter, the analog filter, which is typically an electronic circuit operating on continuous-time analog signals.
A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filter design. The filter is sometimes called a high-cut filter, or treble-cut filter in audio applications. A low-pass filter is the complement of a high-pass filter.
Filter design is the process of designing a signal processing filter that satisfies a set of requirements, some of which may be conflicting. The purpose is to find a realization of the filter that meets each of the requirements to an acceptable degree.
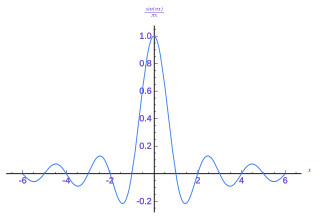
In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and whose frequency response is a sinc function. Calling them according to which domain the filter resembles a sinc avoids confusion. If the domain is unspecified, sinc-in-time is often assumed, or context hopefully can infer the correct domain.
Analog signal processing is a type of signal processing conducted on continuous analog signals by some analog means. "Analog" indicates something that is mathematically represented as a set of continuous values. This differs from "digital" which uses a series of discrete quantities to represent signal. Analog values are typically represented as a voltage, electric current, or electric charge around components in the electronic devices. An error or noise affecting such physical quantities will result in a corresponding error in the signals represented by such physical quantities.
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response is of finite duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely.
Infinite impulse response (IIR) is a property applying to many linear time-invariant systems that are distinguished by having an impulse response that does not become exactly zero past a certain point but continues indefinitely. This is in contrast to a finite impulse response (FIR) system, in which the impulse response does become exactly zero at times for some finite , thus being of finite duration. Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as IIR systems or IIR filters.
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator. Linear systems typically exhibit features and properties that are much simpler than the nonlinear case. As a mathematical abstraction or idealization, linear systems find important applications in automatic control theory, signal processing, and telecommunications. For example, the propagation medium for wireless communication systems can often be modeled by linear systems.

In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined in the overview below. These properties apply (exactly or approximately) to many important physical systems, in which case the response y(t) of the system to an arbitrary input x(t) can be found directly using convolution: y(t) = (x ∗ h)(t) where h(t) is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication). What's more, there are systematic methods for solving any such system (determining h(t)), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers.
Exponential smoothing or exponential moving average (EMA) is a rule of thumb technique for smoothing time series data using the exponential window function. Whereas in the simple moving average the past observations are weighted equally, exponential functions are used to assign exponentially decreasing weights over time. It is an easily learned and easily applied procedure for making some determination based on prior assumptions by the user, such as seasonality. Exponential smoothing is often used for analysis of time-series data.
In digital signal processing, a cascaded integrator–comb (CIC) is a computationally efficient class of low-pass finite impulse response (FIR) filter that chains N number of integrator and comb filter pairs to form a decimator or interpolator. In a decimating CIC, the input signal is first fed through N integrator stages, followed by a down-sampler, and then N comb stages. An interpolating CIC has the reverse order of this architecture, but with the down-sampler replaced with a zero-stuffer (up-sampler).

In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from percussion instruments; most noticeable are the pre-echos. The term "ringing" is because the output signal oscillates at a fading rate around a sharp transition in the input, similar to a bell after being struck. As with other artifacts, their minimization is a criterion in filter design.
Two dimensional filters have seen substantial development effort due to their importance and high applicability across several domains. In the 2-D case the situation is quite different from the 1-D case, because the multi-dimensional polynomials cannot in general be factored. This means that an arbitrary transfer function cannot generally be manipulated into a form required by a particular implementation. The input-output relationship of a 2-D IIR filter obeys a constant-coefficient linear partial difference equation from which the value of an output sample can be computed using the input samples and previously computed output samples. Because the values of the output samples are fed back, the 2-D filter, like its 1-D counterpart, can be unstable.
A two-dimensional (2D) adaptive filter is very much like a one-dimensional adaptive filter in that it is a linear system whose parameters are adaptively updated throughout the process, according to some optimization approach. The main difference between 1D and 2D adaptive filters is that the former usually take as inputs signals with respect to time, what implies in causality constraints, while the latter handles signals with 2 dimensions, like x-y coordinates in the space domain, which are usually non-causal. Moreover, just like 1D filters, most 2D adaptive filters are digital filters, because of the complex and iterative nature of the algorithms.
In mathematics, a nonrecursive filter only uses input values like x[n − 1], unlike recursive filter where it uses previous output values like y[n − 1].
In signal processing, multidimensional discrete convolution refers to the mathematical operation between two functions f and g on an n-dimensional lattice that produces a third function, also of n-dimensions. Multidimensional discrete convolution is the discrete analog of the multidimensional convolution of functions on Euclidean space. It is also a special case of convolution on groups when the group is the group of n-tuples of integers.
Transfer function filter utilizes the transfer function and the Convolution theorem to produce a filter. In this article, an example of such a filter using finite impulse response is discussed and an application of the filter into real world data is shown.



