
In probability theory and related fields, a stochastic or random process is a mathematical object usually defined as a sequence of random variables, where the index of the sequence has the interpretation of time. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance.

Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes. This field was created and started by the Japanese mathematician Kiyosi Itô during World War II.
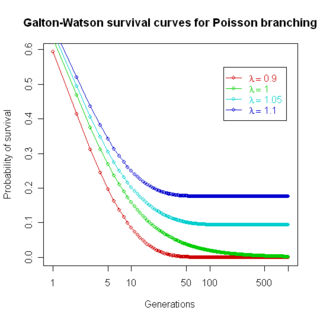
The Galton–Watson process is a branching stochastic process arising from Francis Galton's statistical investigation of the extinction of family names. The process models family names as patrilineal, while offspring are randomly either male or female, and names become extinct if the family name line dies out. This is an accurate description of Y chromosome transmission in genetics, and the model is thus useful for understanding human Y-chromosome DNA haplogroups. Likewise, since mitochondria are inherited only on the maternal line, the same mathematical formulation describes transmission of mitochondria. The formula is of limited usefulness in understanding actual family name distributions, since in practice family names change for many other reasons, and dying out of name line is only one factor.
In population ecology and economics, maximum sustainable yield (MSY) is theoretically, the largest yield that can be taken from a species' stock over an indefinite period. Fundamental to the notion of sustainable harvest, the concept of MSY aims to maintain the population size at the point of maximum growth rate by harvesting the individuals that would normally be added to the population, allowing the population to continue to be productive indefinitely. Under the assumption of logistic growth, resource limitation does not constrain individuals' reproductive rates when populations are small, but because there are few individuals, the overall yield is small. At intermediate population densities, also represented by half the carrying capacity, individuals are able to breed to their maximum rate. At this point, called the maximum sustainable yield, there is a surplus of individuals that can be harvested because growth of the population is at its maximum point due to the large number of reproducing individuals. Above this point, density dependent factors increasingly limit breeding until the population reaches carrying capacity. At this point, there are no surplus individuals to be harvested and yield drops to zero. The maximum sustainable yield is usually higher than the optimum sustainable yield and maximum economic yield.
In probability theory, a branching process is a type of mathematical object known as a stochastic process, which consists of collections of random variables. The random variables of a stochastic process are indexed by the natural numbers. The original purpose of branching processes was to serve as a mathematical model of a population in which each individual in generation produces some random number of individuals in generation , according, in the simplest case, to a fixed probability distribution that does not vary from individual to individual. Branching processes are used to model reproduction; for example, the individuals might correspond to bacteria, each of which generates 0, 1, or 2 offspring with some probability in a single time unit. Branching processes can also be used to model other systems with similar dynamics, e.g., the spread of surnames in genealogy or the propagation of neutrons in a nuclear reactor.

Herbert Ellis Robbins was an American mathematician and statistician. He did research in topology, measure theory, statistics, and a variety of other fields.

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data. Specific mathematical techniques which are used for this include mathematical analysis, linear algebra, stochastic analysis, differential equations, and measure theory.

Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, thought, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior. The mathematical approach is used with the goal of deriving hypotheses that are more exact and thus yield stricter empirical validations. There are five major research areas in mathematical psychology: learning and memory, perception and psychophysics, choice and decision-making, language and thinking, and measurement and scaling.
A stochastic simulation is a simulation of a system that has variables that can change stochastically (randomly) with individual probabilities.
Franz Thomas Bruss is Emeritus Professor of Mathematics at the Université Libre de Bruxelles, where he had been director of "Mathématiques Générales" and co-director of the probability chair, and where he continues his research as invited professor. His main research activities in mathematics are in the field of probability:
Mechanistic models for niche apportionment are biological models used to explain relative species abundance distributions. These niche apportionment models describe how species break up resource pool in multi-dimensional space, determining the distribution of abundances of individuals among species. The relative abundances of species are usually expressed as a Whittaker plot, or rank abundance plot, where species are ranked by number of individuals on the x-axis, plotted against the log relative abundance of each species on the y-axis. The relative abundance can be measured as the relative number of individuals within species or the relative biomass of individuals within species.
In queueing theory, a discipline within the mathematical theory of probability, an M/G/1 queue is a queue model where arrivals are Markovian, service times have a General distribution and there is a single server. The model name is written in Kendall's notation, and is an extension of the M/M/1 queue, where service times must be exponentially distributed. The classic application of the M/G/1 queue is to model performance of a fixed head hard disk.
The Borel distribution is a discrete probability distribution, arising in contexts including branching processes and queueing theory. It is named after the French mathematician Émile Borel.
In mathematics and telecommunications, stochastic geometry models of wireless networks refer to mathematical models based on stochastic geometry that are designed to represent aspects of wireless networks. The related research consists of analyzing these models with the aim of better understanding wireless communication networks in order to predict and control various network performance metrics. The models require using techniques from stochastic geometry and related fields including point processes, spatial statistics, geometric probability, percolation theory, as well as methods from more general mathematical disciplines such as geometry, probability theory, stochastic processes, queueing theory, information theory, and Fourier analysis.
The theorem of the envelopment of societies for resource-dependent populations, also called the Bruss–Duerinckx theorem, is a mathematical result on the behavior of populations that choose their society form according to only two hypotheses that they see as most "natural":
In queueing theory, a discipline within the mathematical theory of probability, a rational arrival process (RAP) is a mathematical model for the time between job arrivals to a system. It extends the concept of a Markov arrival process, allowing for dependent matrix-exponential distributed inter-arrival times.
Stochastic scheduling concerns scheduling problems involving random attributes, such as random processing times, random due dates, random weights, and stochastic machine breakdowns. Major applications arise in manufacturing systems, computer systems, communication systems, logistics and transportation, and machine learning, among others.
Peter Jagers is a Professor Emeritus of Mathematical Statistics at University of Gothenburg and Chalmers University of Technology who made lasting contributions in probability and general branching processes. Jagers was first vice president (2007–2010) of the Royal Swedish Academy of Sciences and Chair of the Royal Society of Arts and Sciences in Gothenburg (2012). He in an elected member of the International Statistical Institute, a Fellow of the Institute of Mathematical Statistics and past President of the Bernoulli Society (2005–2007). He also served as a member of the Scientific Advisory Board of Statistics Sweden.





