In quantum mechanics, a Hamiltonian is an operator corresponding to the sum of the kinetic energies plus the potential energies for all the particles in the system. It is usually denoted by H, also Ȟ or Ĥ. Its spectrum is the set of possible outcomes when one measures the total energy of a system. Because of its close relation to the time-evolution of a system, it is of fundamental importance in most formulations of quantum theory.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can usually be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics. Furthermore, it is one of the few quantum-mechanical systems for which an exact, analytical solution is known.
In physics, specifically in quantum mechanics, a coherent state is the specific quantum state of the quantum harmonic oscillator, often described as a state which has dynamics most closely resembling the oscillatory behavior of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger derived it in 1926, while searching for solutions of the Schrödinger equation that satisfy the correspondence principle. The quantum harmonic oscillator and hence, the coherent states arise in the quantum theory of a wide range of physical systems. For instance, a coherent state describes the oscillating motion of a particle confined in a quadratic potential well. The coherent state describes a state in a system for which the ground-state wavepacket is displaced from the origin of the system. This state can be related to classical solutions by a particle oscillating with an amplitude equivalent to the displacement.
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an additional "perturbing" Hamiltonian representing a weak disturbance to the system. If the disturbance is not too large, the various physical quantities associated with the perturbed system can be expressed as "corrections" to those of the simple system. These corrections, being small compared to the size of the quantities themselves, can be calculated using approximate methods such as asymptotic series. The complicated system can therefore be studied based on knowledge of the simpler one. In effect, it is describing a complicated unsolved system using a simple, solved system.
In quantum mechanics, the particle in a one-dimensional lattice is a problem that occurs in the model of a periodic crystal lattice. The potential is caused by ions in the periodic structure of the crystal creating an electromagnetic field so electrons are subject to a regular potential inside the lattice. This is an extension of the free electron model that assumes zero potential inside the lattice.

In physics, the Rabi cycle is the cyclic behaviour of a two-level quantum system in the presence of an oscillatory driving field. A great variety of physical processes belonging to the areas of quantum computing, condensed matter, atomic and molecular physics, and nuclear and particle physics can be conveniently studied in terms of two-level quantum mechanical systems, and exhibit Rabi flopping when coupled to an oscillatory driving field. The effect is important in quantum optics, magnetic resonance and quantum computing, and is named after Isidor Isaac Rabi.

In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887 laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.
The adiabatic theorem is a concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock (1928), was stated as follows:

In physics, the Lamb shift, named after Willis Lamb, is a difference in energy between two energy levels 2S1/2 and 2P1/2 of the hydrogen atom which was not predicted by the Dirac equation, according to which these states should have the same energy.
The Curie–Weiss law describes the magnetic susceptibility χ of a ferromagnet in the paramagnetic region above the Curie point:
In particle physics, neutral particle oscillation is the transmutation of a particle with zero electric charge into another neutral particle due to a change of a non-zero internal quantum number via an interaction that does not conserve that quantum number. For example, a neutron cannot transmute into an antineutron as that would violate the conservation of baryon number.

The Jaynes–Cummings model is a theoretical model in quantum optics. It describes the system of a two-level atom interacting with a quantized mode of an optical cavity, with or without the presence of light. It was originally developed to study the interaction of atoms with the quantized electromagnetic field in order to investigate the phenomena of spontaneous emission and absorption of photons in a cavity.
Landau quantization in quantum mechanics is the quantization of the cyclotron orbits of charged particles in magnetic fields. As a result, the charged particles can only occupy orbits with discrete energy values, called Landau levels. The Landau levels are degenerate, with the number of electrons per level directly proportional to the strength of the applied magnetic field. Landau quantization is directly responsible for oscillations in electronic properties of materials as a function of the applied magnetic field. It is named after the Soviet physicist Lev Landau.
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. An individual photon can be described as having right or left circular polarization, or a superposition of the two. Equivalently, a photon can be described as having horizontal or vertical linear polarization, or a superposition of the two.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
This article relates the Schrödinger equation with the path integral formulation of quantum mechanics using a simple nonrelativistic one-dimensional single-particle Hamiltonian composed of kinetic and potential energy.
The electron-longitudinal acoustic phonon interaction is an equation concerning atoms.
The fractional Schrödinger equation is a fundamental equation of fractional quantum mechanics. It was discovered by Nick Laskin (1999) as a result of extending the Feynman path integral, from the Brownian-like to Lévy-like quantum mechanical paths. The term fractional Schrödinger equation was coined by Nick Laskin.
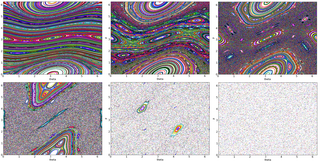
The kicked rotator, also spelled as kicked rotor, is a prototype model for chaos and quantum chaos studies. It describes a particle that is constrained to move on a ring. The particle is kicked periodically by an homogeneous field. The model is described by the Hamiltonian

































