Secondary vector bundle structure

Last updated February 21, 2019

In mathematics, particularly differential topology, the secondary vector bundle structure refers to the natural vector bundle structure $(TE, p *, TM)$ on the total space TE of the tangent bundle of a smooth vector bundle $(E, p, M)$ , induced by the push-forward $p * : TE \to TM$ of the original projection map $p : E \to M$ . This gives rise to a double vector bundle structure $(TE, E, TM, M)$ .

Mathematics includes the study of such topics as quantity, structure, space, and change.

In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.

In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V(x) in such a way that these vector spaces fit together to form another space of the same kind as X, which is then called a vector bundle over X.

In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle (TTM,π_TTM,TM) of the total space TM of the tangent bundle (TM,π_TM,M) of a smooth manifold M . A note on notation: in this article, we denote projection maps by their domains, e.g., π_TTM : TTM → TM. Some authors index these maps by their ranges instead, so for them, that map would be written π_TM.

In differential geometry, the tangent bundle of a differentiable manifold $is a manifold which assembles all the tangent vectors in M . As a set, it is given by the disjoint union of the tangent spaces of M . That is,$

Construction of the secondary vector bundle structure

Let $(E, p, M)$ be a smooth vector bundle of rank $N$ . Then the preimage $(p *) -1 (X) \subset TE$ of any tangent vector $X$ in $TM$ in the push-forward $p * : TE \to TM$ of the canonical projection $p : E \to M$ is a smooth submanifold of dimension $2 N$ , and it becomes a vector space with the push-forwards

+_{*}:T(E\times E)\to TE,\qquad \lambda _{*}:TE\to TE

of the original addition and scalar multiplication

+:E\times E\to E,\qquad \lambda :E\to E

as its vector space operations. The triple $(TE, p *, TM)$ becomes a smooth vector bundle with these vector space operations on its fibres.

Proof

Let $(U, φ)$ be a local coordinate system on the base manifold $M$ with $φ (x) = (x 1, ..., x n)$ and let

{\begin{cases}\psi :W\to \varphi (U)\times \mathbf {R} ^{N}\\\psi \left(v^{k}e_{k}|_{x}\right):=\left(x^{1},\ldots ,x^{n},v^{1},\ldots ,v^{N}\right)\end{cases}}

be a coordinate system on $W:=p^{-1}(U)\subset E$ adapted to it. Then

p_{*}\left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v}+Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v}\right)=X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{p(v)},

so the fiber of the secondary vector bundle structure at $X$ in $T x M$ is of the form

p_{*}^{-1}(X)=\left\{X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v}+Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v}\ :\ v\in E_{x};Y^{1},\ldots ,Y^{N}\in \mathbf {R} \right\}.

Now it turns out that

\chi \left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v}+Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v}\right)=\left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{p(v)},\left(v^{1},\ldots ,v^{N},Y^{1},\ldots ,Y^{N}\right)\right)

gives a local trivialization $χ : TW \to TU \times R 2 N$ for $(TE, p *, TM)$ , and the push-forwards of the original vector space operations read in the adapted coordinates as

\left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v}+Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v}\right)+_{*}\left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{w}+Z^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{w}\right)=X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v+w}+(Y^{\ell }+Z^{\ell }){\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v+w}

and

\lambda _{*}\left(X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{v}+Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{v}\right)=X^{k}{\frac {\partial }{\partial x^{k}}}{\Bigg |}_{\lambda v}+\lambda Y^{\ell }{\frac {\partial }{\partial v^{\ell }}}{\Bigg |}_{\lambda v},

so each fibre $(p *) -1 (X) \subset TE$ is a vector space and the triple $(TE, p *, TM)$ is a smooth vector bundle.

Linearity of connections on vector bundles

The general Ehresmann connection $TE = HE \oplus VE$ on a vector bundle $(E, p, M)$ can be characterized in terms of the connector map

In differential geometry, an Ehresmann connection is a version of the notion of a connection, which makes sense on any smooth fiber bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fiber bundle, but nevertheless, linear connections may be viewed as a special case. Another important special case of Ehresmann connections are principal connections on principal bundles, which are required to be equivariant in the principal Lie group action.

{\begin{cases}\kappa :T_{v}E\to E_{p(v)}\\\kappa (X):=\operatorname {vl} _{v}^{-1}(\operatorname {vpr} X)\end{cases}}

where $vl v : E \to V v E$ is the vertical lift, and $vpr v : T v E \to V v E$ is the vertical projection. The mapping

{\begin{cases}\nabla :\Gamma (TM)\times \Gamma (E)\to \Gamma (E)\\\nabla _{X}v:=\kappa (v_{*}X)\end{cases}}

induced by an Ehresmann connection is a covariant derivative on $Γ(E)$ in the sense that

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean derivative along a tangent vector onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.

{\begin{aligned}\nabla _{X+Y}v&=\nabla _{X}v+\nabla _{Y}v\\\nabla _{\lambda X}v&=\lambda \nabla _{X}v\\\nabla _{X}(v+w)&=\nabla _{X}v+\nabla _{X}w\\\nabla _{X}(\lambda v)&=\lambda \nabla _{X}v\\\nabla _{X}(fv)&=X[f]v+f\nabla _{X}v\end{aligned}}

if and only if the connector map is linear with respect to the secondary vector bundle structure $(TE, p *, TM)$ on $TE$ . Then the connection is called linear. Note that the connector map is automatically linear with respect to the tangent bundle structure $(TE, π TE, E)$ .

Related Research Articles

Vector field assignment of a vector to each point in a subset of Euclidean space

In vector calculus and physics, a vector field is an assignment of a vector to each point in a subset of space. A vector field in the plane, can be visualised as: a collection of arrows with a given magnitude and direction, each attached to a point in the plane. Vector fields are often used to model, for example, the speed and direction of a moving fluid throughout space, or the strength and direction of some force, such as the magnetic or gravitational force, as it changes from one point to another point.

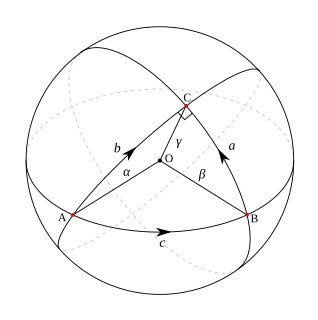
In differential geometry, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints. The great advantage of this method is that it allows the optimization to be solved without explicit parameterization in terms of the constraints. As a result, the method of Lagrange multipliers is widely used to solve challenging constrained optimization problems.

In the mathematical field of differential geometry, a metric tensor is a type of function which takes as input a pair of tangent vectors $v$ and $w$ at a point of a surface and produces a real number scalar $g (v, w)$ in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean space. In the same way as a dot product, metric tensors are used to define the length of and angle between tangent vectors. Through integration, the metric tensor allows one to define and compute the length of curves on the manifold.

In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume of a narrow conical piece of a small geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space. As such, it provides one way of measuring the degree to which the geometry determined by a given Riemannian metric might differ from that of ordinary Euclidean $n$ -space. The Ricci tensor is defined on any pseudo-Riemannian manifold, as a trace of the Riemann curvature tensor. Like the metric itself, the Ricci tensor is a symmetric bilinear form on the tangent space of the manifold.

In differential geometry, the Lie derivative, named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a tensor field, along the flow defined by another vector field. This change is coordinate invariant and therefore the Lie derivative is defined on any differentiable manifold.

In mathematics, the Hodge star operator or Hodge star is a linear map introduced by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented vector space endowed with a nondegenerate symmetric bilinear form. The result when applied to an element of the algebra is called the element's Hodge dual.

In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold $M$ where a Minkowski functional $F (x,-)$ is provided on each tangent space $T x M$ , allowing to define the length of any smooth curve $γ : [a, b] \to M$ as

In physics, a covariant transformation is a rule that specifies how certain entities, such as vectors or tensors, change under a change of basis. The transformation that describes the new basis vectors as a linear combination of the old basis vectors is defined as a covariant transformation. Conventionally, indices identifying the basis vectors are placed as lower indices and so are all entities that transform in the same way. The inverse of a covariant transformation is a contravariant transformation. Whenever a vector should be invariant under a change of basis, that is to say it should represent the same geometrical or physical object having the same magnitude and direction as before, its components must transform according to the contravariant rule. Conventionally, indices identifying the components of a vector are placed as upper indices and so are all indices of entities that transform in the same way. The sum over pairwise matching indices of a product with the same lower and upper indices are invariant under a transformation.

The vierbein or tetrad theory much used in theoretical physics is a special case of the application of Cartan connection in four-dimensional manifolds. It applies to metrics of any signature. This section is an approach to tetrads, but written in general terms. In dimensions other than 4, words like triad, pentad, zweibein, fünfbein, elfbein etc. have been used. Vielbein covers all dimensions.

In differential geometry, a spray is a vector field H on the tangent bundle TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→Φ_H^t(ξ)∈TM obey the rule Φ_H^t(λξ)=Φ_H^λt(ξ) in positive reparameterizations. If this requirement is dropped, H is called a semispray.

The mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.

In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves. In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting".

The Kelvin–Stokes theorem, also known as the curl theorem, is a theorem in vector calculus on $R 3$ . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The Kelvin–Stokes theorem is a special case of the “generalized Stokes' theorem.” In particular, a vector field on $R 3$ can be considered as a 1-form in which case curl is the exterior derivative.

In differential geometry, a fibered manifold is surjective submersion of smooth manifolds $Y \to X$ . Locally trivial fibered manifolds are fiber bundles. Therefore, a notion of connection on fibered manifolds provides a general framework of a connection on fiber bundles.

Proximal gradientmethods for learning is an area of research in optimization and statistical learning theory which studies algorithms for a general class of convex regularization problems where the regularization penalty may not be differentiable. One such example is $regularization of the form$

References

P.Michor. Topics in Differential Geometry, American Mathematical Society (2008).

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.