Related Research Articles
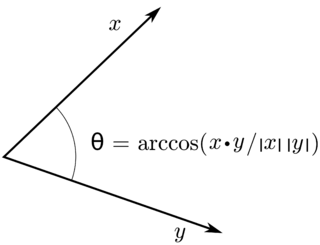
In mathematics, an inner product space is a real vector space or a complex vector space with an operation called an inner product. The inner product of two vectors in the space is a scalar, often denoted with angle brackets such as in . Inner products allow formal definitions of intuitive geometric notions, such as lengths, angles, and orthogonality of vectors. Inner product spaces generalize Euclidean vector spaces, in which the inner product is the dot product or scalar product of Cartesian coordinates. Inner product spaces of infinite dimension are widely used in functional analysis. Inner product spaces over the field of complex numbers are sometimes referred to as unitary spaces. The first usage of the concept of a vector space with an inner product is due to Giuseppe Peano, in 1898.
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space (named after Andrey Kolmogorov) if for every pair of distinct points of X, at least one of them has a neighborhood not containing the other. In a T0 space, all points are topologically distinguishable.
In functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces. All Banach and Hilbert spaces are Fréchet spaces. Spaces of infinitely differentiable functions are typical examples of Fréchet spaces, many of which are typically not Banach spaces.
In mathematics, particularly in functional analysis, a seminorm is a norm that need not be positive definite. Seminorms are intimately connected with convex sets: every seminorm is the Minkowski functional of some absorbing disk and, conversely, the Minkowski functional of any such set is a seminorm.
In functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space , such that the functional sending an operator to the complex number is continuous for any vectors and in the Hilbert space.
In functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the locally convex topology on the set of bounded operators on a Hilbert space H induced by the seminorms of the form , as x varies in H.
In the mathematical field of functional analysis there are several standard topologies which are given to the algebra B(X) of bounded linear operators on a Banach space X.
In functional analysis and related areas of mathematics, locally convex topological vector spaces (LCTVS) or locally convex spaces are examples of topological vector spaces (TVS) that generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of balanced, absorbent, convex sets. Alternatively they can be defined as a vector space with a family of seminorms, and a topology can be defined in terms of that family. Although in general such spaces are not necessarily normable, the existence of a convex local base for the zero vector is strong enough for the Hahn–Banach theorem to hold, yielding a sufficiently rich theory of continuous linear functionals.
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance in a Euclidean space is defined by a norm on the associated Euclidean vector space, called the Euclidean norm, the 2-norm, or, sometimes, the magnitude or length of the vector. This norm can be defined as the square root of the inner product of a vector with itself.
In mathematics, nuclear spaces are topological vector spaces that can be viewed as a generalization of finite-dimensional Euclidean spaces and share many of their desirable properties. Nuclear spaces are however quite different from Hilbert spaces, another generalization of finite-dimensional Euclidean spaces. They were introduced by Alexander Grothendieck.
In mathematics, there are usually many different ways to construct a topological tensor product of two topological vector spaces. For Hilbert spaces or nuclear spaces there is a simple well-behaved theory of tensor products, but for general Banach spaces or locally convex topological vector spaces the theory is notoriously subtle.
In functional analysis, the ultrastrong topology, or σ-strong topology, or strongest topology on the set B(H) of bounded operators on a Hilbert space is the topology defined by the family of seminorms for positive elements of the predual that consists of trace class operators.
In mathematics, in the field of functional analysis, an indefinite inner product space
In linear algebra, functional analysis and related areas of mathematics, a quasinorm is similar to a norm in that it satisfies the norm axioms, except that the triangle inequality is replaced by for some
In operator theory, a branch of mathematics, a positive-definite kernel is a generalization of a positive-definite function or a positive-definite matrix. It was first introduced by James Mercer in the early 20th century, in the context of solving integral operator equations. Since then, positive-definite functions and their various analogues and generalizations have arisen in diverse parts of mathematics. They occur naturally in Fourier analysis, probability theory, operator theory, complex function-theory, moment problems, integral equations, boundary-value problems for partial differential equations, machine learning, embedding problem, information theory, and other areas.
In mathematics, an asymmetric norm on a vector space is a generalization of the concept of a norm.
In probability theory, the multidimensional Chebyshev's inequality is a generalization of Chebyshev's inequality, which puts a bound on the probability of the event that a random variable differs from its expected value by more than a specified amount.
This is a glossary for the terminology in a mathematical field of functional analysis.
In mathematics, specifically in functional analysis and Hilbert space theory, the fundamental theorem of Hilbert spaces gives a necessarily and sufficient condition for a Hausdorff pre-Hilbert space to be a Hilbert space in terms of the canonical isometry of a pre-Hilbert space into its anti-dual.
References
 | This mathematical analysis–related article is a stub. You can help Wikipedia by expanding it. |
 | This linear algebra-related article is a stub. You can help Wikipedia by expanding it. |