
In mathematics and computational geometry, a Delaunay triangulation for a given set P of discrete points in a plane is a triangulation DT(P) such that no point in P is inside the circumcircle of any triangle in DT(P). Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the triangulation; they tend to avoid sliver triangles. The triangulation is named after Boris Delaunay for his work on this topic from 1934.
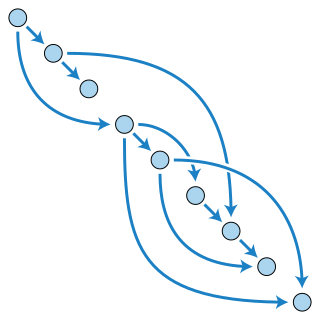
In mathematics, particularly graph theory, and computer science, a directed acyclic graph is a directed graph with no directed cycles. That is, it consists of vertices and edges, with each edge directed from one vertex to another, such that there is no way to start at any vertex v and follow a consistently-directed sequence of edges that eventually loops back to v again. Equivalently, a DAG is a directed graph that has a topological ordering, a sequence of the vertices such that every edge is directed from earlier to later in the sequence.

The Steiner tree problem, or minimum Steiner tree problem, named after Jakob Steiner, is an umbrella term for a class of problems in combinatorial optimization. While Steiner tree problems may be formulated in a number of settings, they all require an optimal interconnect for a given set of objects and a predefined objective function. One well-known variant, which is often used synonymously with the term Steiner tree problem, is the Steiner tree problem in graphs. Given an undirected graph with non-negative edge weights and a subset of vertices, usually referred to as terminals, the Steiner tree problem in graphs requires a tree of minimum weight that contains all terminals. Further well-known variants are the Euclidean Steiner tree problem and the rectilinear minimum Steiner tree problem.

In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is P.

The Euclidean minimum spanning tree or EMST is a minimum spanning tree of a set of n points in the plane, where the weight of the edge between each pair of points is the Euclidean distance between those two points. In simpler terms, an EMST connects a set of dots using lines such that the total length of all the lines is minimized and any dot can be reached from any other by following the lines.

In geometry, a simple polygon is a polygon that does not intersect itself and has no holes. That is, it is a flat shape consisting of straight, non-intersecting line segments or "sides" that are joined pairwise to form a single closed path. If the sides intersect then the polygon is not simple. The qualifier "simple" is frequently omitted, with the above definition then being understood to define a polygon in general.
A Steiner point may refer to:

The k-minimum spanning tree problem, studied in theoretical computer science, asks for a tree of minimum cost that has exactly k vertices and forms a subgraph of a larger graph. It is also called the k-MST or edge-weighted k-cardinality tree. Finding this tree is NP-hard, but it can be approximated to within a constant approximation ratio in polynomial time.
In geometry, a triangulation is a subdivision of a planar object into triangles, and by extension the subdivision of a higher-dimension geometric object into simplices. Triangulations of a three-dimensional volume would involve subdividing it into tetrahedra packed together.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. The goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.
The Christofides algorithm or Christofides–Serdyukov algorithm is an algorithm for finding approximate solutions to the travelling salesman problem, on instances where the distances form a metric space . It is an approximation algorithm that guarantees that its solutions will be within a factor of 3/2 of the optimal solution length, and is named after Nicos Christofides and Anatoliy I. Serdyukov, who discovered it independently in 1976.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.

In graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest.
In computational geometry, the Bentley–Ottmann algorithm is a sweep line algorithm for listing all crossings in a set of line segments, i.e. it finds the intersection points of line segments. It extends the Shamos–Hoey algorithm, a similar previous algorithm for testing whether or not a set of line segments has any crossings. For an input consisting of line segments with crossings, the Bentley–Ottmann algorithm takes time . In cases where , this is an improvement on a naïve algorithm that tests every pair of segments, which takes .
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
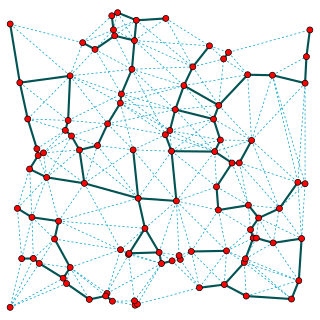
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
The rectilinear Steiner tree problem, minimum rectilinear Steiner tree problem (MRST), or rectilinear Steiner minimum tree problem (RSMT) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance is replaced with the rectilinear distance. The problem may be formally stated as follows: given n points in the plane, it is required to interconnect them all by a shortest network which consists only of vertical and horizontal line segments. It can be shown that such a network is a tree whose vertices are the input points plus some extra points.
A covering of a polygon is a set of primitive units whose union equals the polygon. A polygon covering problem is a problem of finding a covering with a smallest number of units for a given polygon. This is an important class of problems in computational geometry. There are many different polygon covering problems, depending on the type of polygon being covered and on the types of units allowed in the covering. An example polygon covering problem is: given a rectilinear polygon, find a smallest set of squares whose union equals the polygon.
A partition of a polygon is a set of primitive units, which do not overlap and whose union equals the polygon. A polygon partition problem is a problem of finding a partition which is minimal in some sense, for example a partition with a smallest number of units or with units of smallest total side-length.











