
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally,
In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful for efficient numerical solutions, e.g. Monte Carlo simulations. It was discovered by André-Louis Cholesky for real matrices. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.
In the mathematical discipline of linear algebra, a matrix decomposition or matrix factorization is a factorization of a matrix into a product of matrices. There are many different matrix decompositions; each finds use among a particular class of problems.
Bruun's algorithm is a fast Fourier transform (FFT) algorithm based on an unusual recursive polynomial-factorization approach, proposed for powers of two by G. Bruun in 1978 and generalized to arbitrary even composite sizes by H. Murakami in 1996. Because its operations involve only real coefficients until the last computation stage, it was initially proposed as a way to efficiently compute the discrete Fourier transform (DFT) of real data. Bruun's algorithm has not seen widespread use, however, as approaches based on the ordinary Cooley–Tukey FFT algorithm have been successfully adapted to real data with at least as much efficiency. Furthermore, there is evidence that Bruun's algorithm may be intrinsically less accurate than Cooley–Tukey in the face of finite numerical precision.

In numerical analysis and computer science, a sparse matrix or sparse array is a matrix in which most of the elements are zero. By contrast, if most of the elements are nonzero, then the matrix is considered dense. The number of zero-valued elements divided by the total number of elements is called the sparsity of the matrix. Using those definitions, a matrix will be sparse when its sparsity is greater than 0.5.
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements only on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.
In numerical analysis the minimum degree algorithm is an algorithm used to permute the rows and columns of a symmetric sparse matrix before applying the Cholesky decomposition, to reduce the number of non-zeros in the Cholesky factor.
This results in reduced storage requirements and means that the Cholesky factor, or sometimes an incomplete Cholesky factor used as a preconditioner can be applied with fewer arithmetic operations.
In mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.

In mathematics and especially in combinatorics, a plane partition is a two-dimensional array of nonnegative integers
that is nonincreasing in both indices. This means that
In numerical analysis and linear algebra, lower–upper (LU) decomposition or factorization factors a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. LU decomposition can be viewed as the matrix form of Gaussian elimination. Computers usually solve square systems of linear equations using LU decomposition, and it is also a key step when inverting a matrix or computing the determinant of a matrix. LU decomposition was introduced by mathematician Tadeusz Banachiewicz in 1938.
Numerical linear algebra is the study of how matrix operations can be used to create computer algorithms which efficiently and accurately provide approximate answers to mathematical questions. It is a subfield of numerical analysis, and a type of linear algebra. Because computers use floating-point arithmetic, they cannot exactly represent irrational data, and many algorithms increase that imprecision when implemented by a computer. Numerical linear algebra uses properties of vectors and matrices to develop computer algorithms that minimize computer error while retaining efficiency and precision.
In numerical linear algebra, an incomplete LU factorization of a matrix is a sparse approximation of the LU factorization often used as a preconditioner.
In numerical analysis, an incomplete Cholesky factorization of a symmetric positive definite matrix is a sparse approximation of the Cholesky factorization. An incomplete Cholesky factorization is often used as a preconditioner for algorithms like the conjugate gradient method.
In mathematics, Sylvester’s criterion is a necessary and sufficient criterion to determine whether a Hermitian matrix is positive-definite. It is named after James Joseph Sylvester.
In multilinear algebra, the tensor rank decomposition or canonical polyadic decomposition (CPD) may be regarded as a generalization of the matrix singular value decomposition (SVD) to tensors, which has found application in statistics, signal processing, psychometrics, linguistics and chemometrics. It was introduced by Hitchcock in 1927 and later rediscovered several times, notably in psychometrics.
For this reason, the tensor rank decomposition is sometimes historically referred to as PARAFAC or CANDECOMP.
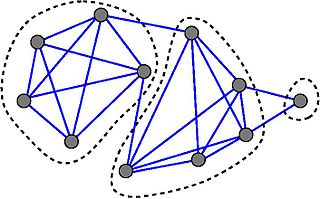
In the branch of mathematics called graph theory, the strength of an undirected graph corresponds to the minimum ratio edges removed/components created in a decomposition of the graph in question. It is a method to compute partitions of the set of vertices and detect zones of high concentration of edges, and is analogous to graph toughness which is defined similarly for vertex removal.
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
In numerical analysis, nested dissection is a divide and conquer heuristic for the solution of sparse symmetric systems of linear equations based on graph partitioning. Nested dissection was introduced by George (1973); the name was suggested by Garrett Birkhoff.
In numerical mathematics, hierarchical matrices (H-matrices)
are used as data-sparse approximations of non-sparse matrices.
While a sparse matrix of dimension
can be represented efficiently in
units of storage
by storing only its non-zero entries, a non-sparse matrix would require
units of storage, and using this type
of matrices for large problems would therefore be prohibitively expensive in terms of storage and computing time.
Hierarchical matrices provide an approximation requiring only
units of storage, where
is a
parameter controlling the accuracy of the approximation.
In typical applications, e.g., when discretizing integral equations
,
preconditioning the resulting systems of linear equations
,
or solving elliptic partial differential equations
,
a rank proportional to
with a small constant
is sufficient to ensure an
accuracy of
.
Compared to many other data-sparse representations of non-sparse matrices, hierarchical matrices offer a major advantage:
the results of matrix arithmetic operations like matrix multiplication, factorization or inversion can be approximated
in
operations, where

In applied mathematics, K-SVD is a dictionary learning algorithm for creating a dictionary for sparse representations, via a singular value decomposition approach. K-SVD is a generalization of the k-means clustering method, and it works by iteratively alternating between sparse coding the input data based on the current dictionary, and updating the atoms in the dictionary to better fit the data. K-SVD can be found widely in use in applications such as image processing, audio processing, biology, and document analysis.
















