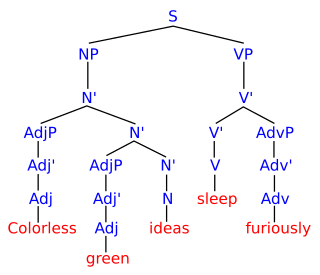
In mathematics, computer science, and linguistics, a formal language consists of words whose letters are taken from an alphabet and are well-formed according to a specific set of rules.
In mathematics, a finite set is a set that has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting. For example,
In mathematics, model theory is the study of the relationship between formal theories, and their models, taken as interpretations that satisfy the sentences of that theory.
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of these outcomes is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes, which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion. Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability theory describing such behaviour are the law of large numbers and the central limit theorem.
Inductive logic programming (ILP) is a subfield of symbolic artificial intelligence which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.
In programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and mathematical proofs.
Computability logic (CoL) is a research program and mathematical framework for redeveloping logic as a systematic formal theory of computability, as opposed to classical logic which is a formal theory of truth. It was introduced and so named by Giorgi Japaridze in 2003.
Game semantics is an approach to formal semantics that grounds the concepts of truth or validity on game-theoretic concepts, such as the existence of a winning strategy for a player, somewhat resembling Socratic dialogues or medieval theory of Obligationes.
Interpretability logics comprise a family of modal logics that extend provability logic to describe interpretability or various related metamathematical properties and relations such as weak interpretability, Π1-conservativity, cointerpretability, tolerance, cotolerance, and arithmetic complexities.
Provability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic.
In mathematical logic, interpretability is a relation between formal theories that expresses the possibility of interpreting or translating one into the other.
In mathematical logic, cointerpretability is a binary relation on formal theories: a formal theory T is cointerpretable in another such theory S, when the language of S can be translated into the language of T in such a way that S proves every formula whose translation is a theorem of T. The "translation" here is required to preserve the logical structure of formulas.
In mathematical logic, weak interpretability is a notion of translation of logical theories, introduced together with interpretability by Alfred Tarski in 1953.
Giorgi Japaridze is a Georgian-American researcher in logic and theoretical computer science. He currently holds the title of Full Professor at the Computing Sciences Department of Villanova University. Japaridze is best known for his invention of computability logic, cirquent calculus, and Japaridze's polymodal logic.
The notion of institution was created by Joseph Goguen and Rod Burstall in the late 1970s, in order to deal with the "population explosion among the logical systems used in computer science". The notion tries to capture the essence of the concept of "logical system".
In mathematics, Kruskal's tree theorem states that the set of finite trees over a well-quasi-ordered set of labels is itself well-quasi-ordered under homeomorphic embedding. The theorem was conjectured by Andrew Vázsonyi and proved by Joseph Kruskal (1960); a short proof was given by Nash-Williams (1963). It has since become a prominent example in reverse mathematics as a statement that cannot be proved within ATR0 (a form of arithmetical transfinite recursion), and a finitary application of the theorem gives the existence of the notoriously fast-growing TREE function.
In mathematical logic, an ω-consistenttheory is a theory that is not only (syntactically) consistent, but also avoids proving certain infinite combinations of sentences that are intuitively contradictory. The name is due to Kurt Gödel, who introduced the concept in the course of proving the incompleteness theorem.
Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. The same first-order language with "" and "" of classical set theory is usually used, so this is not to be confused with a constructive types approach. On the other hand, some constructive theories are indeed motivated by their interpretability in type theories.
Revision theory is a subfield of philosophical logic. It consists of a general theory of definitions, including circular and interdependent concepts. A circular definition is one in which the concept being defined occurs in the statement defining it—for example, defining a G as being blue and to the left of a G. Revision theory provides formal semantics for defined expressions, and formal proof systems study the logic of circular expressions.
Japaridze's polymodal logic (GLP), is a system of provability logic with infinitely many provability modalities. This system has played an important role in some applications of provability algebras in proof theory, and has been extensively studied since the late 1980s. It is named after Giorgi Japaridze.







