
The Cauchy distribution, named after Augustin Cauchy, is a continuous probability distribution. It is also known, especially among physicists, as the Lorentz distribution, Cauchy–Lorentz distribution, Lorentz(ian) function, or Breit–Wigner distribution. The Cauchy distribution is the distribution of the x-intercept of a ray issuing from with a uniformly distributed angle. It is also the distribution of the ratio of two independent normally distributed random variables if the denominator distribution has mean zero.

In mathematics, the gamma function is one of a number of extensions of the factorial function with its argument shifted down by 1, to real and complex numbers. Derived by Daniel Bernoulli, if n is a positive integer,

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, scientific, geophysical, actuarial, and many other types of observable phenomena. Originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population, the Pareto distribution has colloquially become known and referred to as the Pareto principle, or "80-20 rule", and is sometimes called the "Matthew principle". This rule states that, for example, 80% of the wealth of a society is held by 20% of its population. However, the Pareto distribution only produces this result for a particular power value, (α = log45 ≈ 1.16). While is variable, empirical observation has found the 80-20 distribution to fit a wide range of cases, including natural phenomena and human activities.

In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if two different paths connect the same two points, and a function is holomorphic everywhere in between the two paths, then the two path integrals of the function will be the same.

In probability theory and statistics, the chi-squared distribution with k degrees of freedom is the distribution of a sum of the squares of k independent standard normal random variables. The chi-squared distribution is a special case of the gamma distribution and is one of the most widely used probability distributions in inferential statistics, notably in hypothesis testing or in construction of confidence intervals. When it is being distinguished from the more general noncentral chi-squared distribution, this distribution is sometimes called the central chi-squared distribution.

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter gamma.

In mathematics, the n-th harmonic number is the sum of the reciprocals of the first n natural numbers:
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function defined by

In mathematics, the digamma function is defined as the logarithmic derivative of the gamma function:
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals.

In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument.
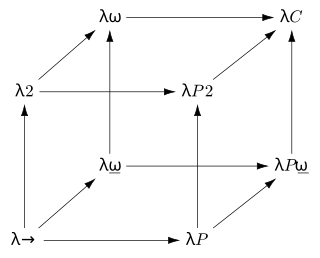
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new way of making objects depend on other objects, namely
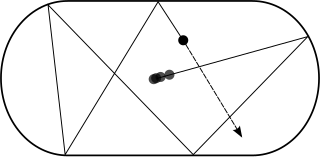
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed. Billiard dynamical systems are Hamiltonian idealizations of the game of billiards, but where the region contained by the boundary can have shapes other than rectangular and even be multidimensional. Dynamical billiards may also be studied on non-Euclidean geometries; indeed, the very first studies of billiards established their ergodic motion on surfaces of constant negative curvature. The study of billiards which are kept out of a region, rather than being kept in a region, is known as outer billiard theory.
The Fransén–Robinson constant, sometimes denoted F, is the mathematical constant that represents the area between the graph of the reciprocal Gamma function, 1 / Γ(x), and the positive x axis. That is,

In mathematics, the reciprocal gamma function is the function
In mathematics, a reflection formula or reflection relation for a function f is a relationship between f(a − x) and f(x). It is a special case of a functional equation, and it is very common in the literature to use the term "functional equation" when "reflection formula" is meant.
In q-analog theory, the -gamma function, or basic gamma function, is a generalization of the ordinary Gamma function closely related to the double gamma function. It was introduced by Jackson (1905). It is given by

In mathematics, the Struve functionsHα(x), are solutions y(x) of the non-homogeneous Bessel's differential equation:
In the geometry of numbers, the Klein polyhedron, named after Felix Klein, is used to generalize the concept of continued fractions to higher dimensions.















