Transportation network may refer to:
 | This disambiguation page lists articles associated with the title Transportation network. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.
In general, a node is a localized swelling or a point of intersection.
Network and networking may refer to:
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.
Graph may refer to:
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
Fan-Rong King Chung Graham, known professionally as Fan Chung, is a Taiwanese-born American mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular in generalizing the Erdős–Rényi model for graphs with general degree distribution.
In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of typical graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, random graph refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a random graph.
Cubic may refer to:
In mathematics, and more specifically in graph theory, a vertex or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges, while a directed graph consists of a set of vertices and a set of arcs. In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another.
In graph theory, a flow network is a directed graph where each edge has a capacity and each edge receives a flow. The amount of flow on an edge cannot exceed the capacity of the edge. Often in operations research, a directed graph is called a network, the vertices are called nodes and the edges are called arcs. A flow must satisfy the restriction that the amount of flow into a node equals the amount of flow out of it, unless it is a source, which has only outgoing flow, or sink, which has only incoming flow. A network can be used to model traffic in a computer network, circulation with demands, fluids in pipes, currents in an electrical circuit, or anything similar in which something travels through a network of nodes.
In the psychology of motivation, balance theory is a theory of attitude change, proposed by Fritz Heider. It conceptualizes the cognitive consistency motive as a drive toward psychological balance. The consistency motive is the urge to maintain one's values and beliefs over time. Heider proposed that "sentiment" or liking relationships are balanced if the affect valence in a system multiplies out to a positive result.
A transport network, or transportation network is a realisation of a spatial network, describing a structure which permits either vehicular movement or flow of some commodity. Examples include but are not limited to road networks, railways, air routes, pipelines, aqueducts, and power lines.
A spatial network is a graph in which the vertices or edges are spatial elements associated with geometric objects, i.e. the nodes are located in a space equipped with a certain metric. The simplest mathematical realization is a lattice or a random geometric graph, where nodes are distributed uniformly at random over a two-dimensional plane; a pair of nodes are connected if the Euclidean distance is smaller than a given neighborhood radius. Transportation and mobility networks, Internet, mobile phone networks, power grids, social and contact networks and biological neural networks are all examples where the underlying space is relevant and where the graph's topology alone does not contain all the information. Characterizing and understanding the structure, resilience and the evolution of spatial networks is crucial for many different fields ranging from urbanism to epidemiology.
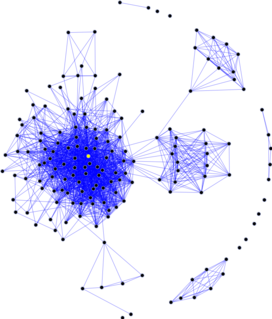
The social graph is a graph that represents social relations between entities. In short, it is a model or representation of a social network, where the word graph has been taken from graph theory. The social graph has been referred to as "the global mapping of everybody and how they're related".
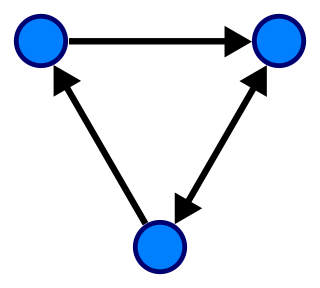
In mathematics, and more specifically in graph theory, a directed graph is a graph that is made up of a set of vertices connected by edges, where the edges have a direction associated with them.
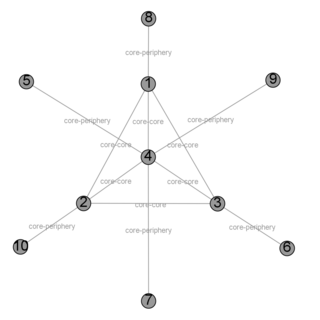
Core periphery structure is a network theory model based on Immanuel Wallerstein's world-systems theory. He formulated the chart in the 1980s.
Air transport network or air transportation network (ATN) is an example of transport networks and spatial networks. The nodes of the network are the airports and the links represent direct flight routes between two airports. Alternatively, cities can be considered as the nodes with links representing direct flight connection between them. Air transport networks can be defined worldwide as well as for one region or for one airline company; the scale of the network can be global or domestic.