
Microeconomics is a branch of mainstream economics that studies the behavior of individuals and firms in making decisions regarding the allocation of scarce resources and the interactions among these individuals and firms. Microeconomics focuses on the study of individual markets, sectors, or industries as opposed to the national economy as whole, which is studied in macroeconomics.

Mathematical optimization or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries.
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints. It is named after the mathematician Joseph-Louis Lagrange. The basic idea is to convert a constrained problem into a form such that the derivative test of an unconstrained problem can still be applied. The relationship between the gradient of the function and gradients of the constraints rather naturally leads to a reformulation of the original problem, known as the Lagrangian function.
The costate equation is related to the state equation used in optimal control. It is also referred to as auxiliary, adjoint, influence, or multiplier equation. It is stated as a vector of first order differential equations

Optimal control theory is a branch of mathematical optimization that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory.
In mathematics, nonlinear programming (NLP) is the process of solving an optimization problem where some of the constraints or the objective function are nonlinear. An optimization problem is one of calculation of the extrema of an objective function over a set of unknown real variables and conditional to the satisfaction of a system of equalities and inequalities, collectively termed constraints. It is the sub-field of mathematical optimization that deals with problems that are not linear.
Pontryagin's maximum principle is used in optimal control theory to find the best possible control for taking a dynamical system from one state to another, especially in the presence of constraints for the state or input controls. It states that it is necessary for any optimal control along with the optimal state trajectory to solve the so-called Hamiltonian system, which is a two-point boundary value problem, plus a maximum condition of the control Hamiltonian. These necessary conditions become sufficient under certain convexity conditions on the objective and constraint functions.
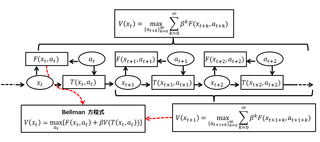
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used.
In mathematical optimization theory, the linear complementarity problem (LCP) arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case. It was proposed by Cottle and Dantzig in 1968.
In mathematical optimization, the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied.
In mathematical optimization theory, duality or the duality principle is the principle that optimization problems may be viewed from either of two perspectives, the primal problem or the dual problem. If the primal is a minimization problem then the dual is a maximization problem. Any feasible solution to the primal (minimization) problem is at least as large as any feasible solution to the dual (maximization) problem. Therefore, the solution to the primal is an upper bound to the solution of the dual, and the solution of the dual is a lower bound to the solution of the primal. This fact is called weak duality.
In mathematical optimization, constrained optimization is the process of optimizing an objective function with respect to some variables in the presence of constraints on those variables. The objective function is either a cost function or energy function, which is to be minimized, or a reward function or utility function, which is to be maximized. Constraints can be either hard constraints, which set conditions for the variables that are required to be satisfied, or soft constraints, which have some variable values that are penalized in the objective function if, and based on the extent that, the conditions on the variables are not satisfied.

The Ramsey–Cass–Koopmans model, or Ramsey growth model, is a neoclassical model of economic growth based primarily on the work of Frank P. Ramsey, with significant extensions by David Cass and Tjalling Koopmans. The Ramsey–Cass–Koopmans model differs from the Solow–Swan model in that the choice of consumption is explicitly microfounded at a point in time and so endogenizes the savings rate. As a result, unlike in the Solow–Swan model, the saving rate may not be constant along the transition to the long run steady state. Another implication of the model is that the outcome is Pareto optimal or Pareto efficient.
The Hamiltonian is a function used to solve a problem of optimal control for a dynamical system. It can be understood as an instantaneous increment of the Lagrangian expression of the problem that is to be optimized over a certain time period. Inspired by, but distinct from, the Hamiltonian of classical mechanics, the Hamiltonian of optimal control theory was developed by Lev Pontryagin as part of his maximum principle. Pontryagin proved that a necessary condition for solving the optimal control problem is that the control should be chosen so as to optimize the Hamiltonian.
In mathematics, a constraint is a condition of an optimization problem that the solution must satisfy. There are several types of constraints—primarily equality constraints, inequality constraints, and integer constraints. The set of candidate solutions that satisfy all constraints is called the feasible set.

In mathematical optimization, a feasible region, feasible set, search space, or solution space is the set of all possible points of an optimization problem that satisfy the problem's constraints, potentially including inequalities, equalities, and integer constraints. This is the initial set of candidate solutions to the problem, before the set of candidates has been narrowed down.
The value function of an optimization problem gives the value attained by the objective function at a solution, while only depending on the parameters of the problem. In a controlled dynamical system, the value function represents the optimal payoff of the system over the interval [t, t1] when started at the time-t state variable x(t)=x. If the objective function represents some cost that is to be minimized, the value function can be interpreted as the cost to finish the optimal program, and is thus referred to as "cost-to-go function." In an economic context, where the objective function usually represents utility, the value function is conceptually equivalent to the indirect utility function.
In mathematical logic, an omega-categorical theory is a theory that has exactly one countably infinite model up to isomorphism. Omega-categoricity is the special case κ = = ω of κ-categoricity, and omega-categorical theories are also referred to as ω-categorical. The notion is most important for countable first-order theories.
The Fritz John conditions, in mathematics, are a necessary condition for a solution in nonlinear programming to be optimal. They are used as lemma in the proof of the Karush–Kuhn–Tucker conditions, but they are relevant on their own.
In optimal control theory, a control is a variable chosen by the controller or agent to manipulate state variables, similar to an actual control valve. Unlike the state variable, it does not have a predetermined equation of motion. The goal of optimal control theory is to find some sequence of controls to achieve an optimal path for the state variables.





