Related Research Articles
In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem is a task solved by a computer. A computation problem is solvable by mechanical application of mathematical steps, such as an algorithm.

In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding by means of an algorithm whether a given natural number is prime. Another is the problem "given two numbers x and y, does x evenly divide y?". The answer is either 'yes' or 'no' depending upon the values of x and y. A method for solving a decision problem, given in the form of an algorithm, is called a decision procedure for that problem. A decision procedure for the decision problem "given two numbers x and y, does x evenly divide y?" would give the steps for determining whether x evenly divides y. One such algorithm is long division. If the remainder is zero the answer is 'yes', otherwise it is 'no'. A decision problem which can be solved by an algorithm is called decidable.
In computational complexity theory, the class NC (for "Nick's Class") is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem with input size n is in NC if there exist constants c and k such that it can be solved in time O((log n)c) using O(nk) parallel processors. Stephen Cook coined the name "Nick's class" after Nick Pippenger, who had done extensive research on circuits with polylogarithmic depth and polynomial size.
In computational complexity theory, a decision problem is P-complete if it is in P and every problem in P can be reduced to it by an appropriate reduction.

Consensus decision-making or consensus process is a group decision-making process in which participants develop and decide on proposals with the goal of achieving broad acceptance, defined by its terms as form of consensus. The focus on establishing agreement of at least the majority or the supermajority and avoiding unproductive opinion differentiates consensus from unanimity, which requires all participants to support a decision. Consensus decision-making in a democracy is consensus democracy.
In computational complexity theory, an advice string is an extra input to a Turing machine that is allowed to depend on the length n of the input, but not on the input itself. A decision problem is in the complexity class P/f(n) if there is a polynomial time Turing machine M with the following property: for any n, there is an advice string A of length f(n) such that, for any input x of length n, the machine M correctly decides the problem on the input x, given x and A.

Buridan's ass is an illustration of a paradox in philosophy in the conception of free will. It refers to a hypothetical situation wherein an ass (donkey) that is equally hungry and thirsty is placed precisely midway between a stack of hay and a pail of water. Since the paradox assumes the donkey will always go to whichever is closer, it dies of both hunger and thirst since it cannot make any rational decision between the hay and water. A common variant of the paradox substitutes the hay and water for two identical piles of hay; the ass, unable to choose between the two, dies of hunger.
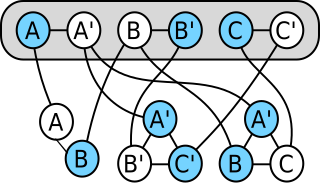
In computability theory and computational complexity theory, a reduction is an algorithm for transforming one problem into another problem. A sufficiently efficient reduction from one problem to another may be used to show that the second problem is at least as difficult as the first.
In computational complexity theory, L is the complexity class containing decision problems that can be solved by a deterministic Turing machine using a logarithmic amount of writable memory space. Formally, the Turing machine has two tapes, one of which encodes the input and can only be read, whereas the other tape has logarithmic size but can be read as well as written. Logarithmic space is sufficient to hold a constant number of pointers into the input and a logarithmic number of boolean flags, and many basic logspace algorithms use the memory in this way.
In computability theory, a decider is a Turing machine that halts for every input. A decider is also called a total Turing machine as it represents a total function.
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer to a problem instance is 'yes', then there is some procedure that takes finite time to determine this, and this procedure never falsely reports 'yes' when the true answer is 'no'. However, when the true answer is 'no', the procedure is not required to halt; it may go into an "infinite loop" for some 'no' cases. Such a procedure is sometimes called a semi-algorithm, to distinguish it from an algorithm, defined as a complete solution to a decision problem.
A distributed algorithm is an algorithm designed to run on computer hardware constructed from interconnected processors. Distributed algorithms are used in different application areas of distributed computing, such as telecommunications, scientific computing, distributed information processing, and real-time process control. Standard problems solved by distributed algorithms include leader election, consensus, distributed search, spanning tree generation, mutual exclusion, and resource allocation.
A fundamental problem in distributed computing and multi-agent systems is to achieve overall system reliability in the presence of a number of faulty processes. This often requires coordinating processes to reach consensus, or agree on some data value that is needed during computation. Example applications of consensus include agreeing on what transactions to commit to a database in which order, state machine replication, and atomic broadcasts. Real-world applications often requiring consensus include cloud computing, clock synchronization, PageRank, opinion formation, smart power grids, state estimation, control of UAVs, load balancing, blockchain, and others.
Control is a function of management that helps to check errors and take corrective actions. This is done to minimize deviation from standards and ensure that the stated goals of the organization are achieved in a desired manner.
In computational complexity theory, the average-case complexity of an algorithm is the amount of some computational resource used by the algorithm, averaged over all possible inputs. It is frequently contrasted with worst-case complexity which considers the maximal complexity of the algorithm over all possible inputs.
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is proved to be impossible to construct an algorithm that always leads to a correct yes-or-no answer. The halting problem is an example: it can be proven that there is no algorithm that correctly determines whether an arbitrary program eventually halts when run.
In computability theory, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running, or continue to run forever. The halting problem is undecidable, meaning that no general algorithm exists that solves the halting problem for all possible program–input pairs. The problem comes up often in discussions of computability since it demonstrates that some functions are mathematically definable but not computable.

A working group is a group of experts working together to achieve specified goals. Such groups are domain-specific and focus on discussion or activity around a specific subject area. The term can sometimes refer to an interdisciplinary collaboration of researchers, often from more than one organization, working on new activities that would be difficult to sustain under traditional funding mechanisms. Working groups are variously also called task groups, workgroups, technical advisory groups, working parties, or task forces.
The Chandra–Toueg consensus algorithm, published by Tushar Deepak Chandra and Sam Toueg in 1996, is an algorithm for solving consensus in a network of unreliable processes equipped with an eventually strong failure detector. The failure detector is an abstract version of timeouts; it signals to each process when other processes may have crashed. An eventually strong failure detector is one that never identifies some specific non-faulty process as having failed after some initial period of confusion, and, at the same time, eventually identifies all faulty processes as failed. The Chandra–Toueg consensus algorithm assumes that the number of faulty processes, denoted by f, is less than n/2, i.e. it assumes f < n/2, where n is the total number of processes.
The general group problem solving model is a problem solving methodology, in which a group of individuals will define the desired outcome, identify the gap between the current state and the target and generate ideas for closing the gap by brainstorming. The result is list of actions needed to achieve the desired results.
References
- Charron-Bost, Bernadette; Schiper, André (April 2004). "Uniform consensus is harder than consensus". Journal of Algorithms. 51 (1): 15–37. doi:10.1016/j.jalgor.2003.11.001.