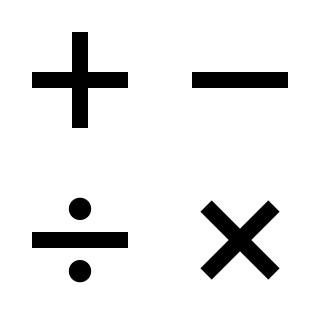In computer science, an array data structure, or simply an array, is a data structure consisting of a collection of elements, each identified by at least one array index or key. An array is stored such that the position of each element can be computed from its index tuple by a mathematical formula. The simplest type of data structure is a linear array, also called one-dimensional array.
In mathematics, a linear map is a mapping V → W between two modules that preserves the operations of addition and scalar multiplication.

In mathematics, a set B of elements (vectors) in a vector space V is called a basis, if every element of V may be written in a unique way as a (finite) linear combination of elements of B. The coefficients of this linear combination are referred to as components or coordinates on B of the vector. The elements of a basis are called basis vectors.

In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed. Like a set, it contains members. The number of elements is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and order matters. Formally, a sequence can be defined as a function whose domain is either the set of the natural numbers or the set of the first n natural numbers. The position of an element in a sequence is its rank or index; it is the natural number from which the element is the image. It depends on the context or a specific convention, if the first element has index 0 or 1. When a symbol has been chosen for denoting a sequence, the nth element of the sequence is denoted by this symbol with n as subscript; for example, the nth element of the Fibonacci sequence is generally denoted Fn.
An exact sequence is a concept in mathematics, especially in group theory, ring and module theory, homological algebra, as well as in differential geometry. An exact sequence is a sequence, either finite or infinite, of objects and morphisms between them such that the image of one morphism equals the kernel of the next.
In the mathematics of the real numbers, the logarithm logba is a number x such that bx = a, for given numbers a and b. Analogously, in any group G, powers bk can be defined for all integers k, and the discrete logarithm logba is an integer k such that bk = a. In number theory, the more commonly used term is index: we can write x = indra for rx ≡ a if r is a primitive root of m and gcd(a,m)=1.
In mathematics, specifically in homology theory and algebraic topology, cohomology is a general term for a sequence of abelian groups associated to a topological space, often defined from a cochain complex. Cohomology can be viewed as a method of assigning richer algebraic invariants to a space than homology. Some versions of cohomology arise by dualizing the construction of homology. In other words, cochains are functions on the group of chains in homology theory.
In mathematics and specifically in algebraic geometry, the dimension of an algebraic variety may be defined in various equivalent ways.
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated addition and exponentiation as iterated multiplication. Continuing in this manner leads to tetration and to the remainder of the hyperoperation sequence, which is commonly denoted using Knuth arrow notation. This notation allows for a simple description of numbers far larger than can be explicitly written out.
In mathematics and computer programming, index notation is used to specify the elements of an array of numbers. The formalism of how indices are used varies according to the subject. In particular, there are different methods for referring to the elements of a list, a vector, or a matrix, depending on whether one is writing a formal mathematical paper for publication, or when one is writing a computer program.

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers. It was developed by Arnold Schönhage and Volker Strassen in 1971. The run-time bit complexity is, in Big O notation, for two n-digit numbers. The algorithm uses recursive Fast Fourier transforms in rings with 2n+1 elements, a specific type of number theoretic transform.
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid M in the most universal way in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from the more general construction in category theory, introduced by Alexander Grothendieck in his fundamental work of the mid-1950s that resulted in the development of K-theory, which led to his proof of the Grothendieck–Riemann–Roch theorem. This article treats both constructions.
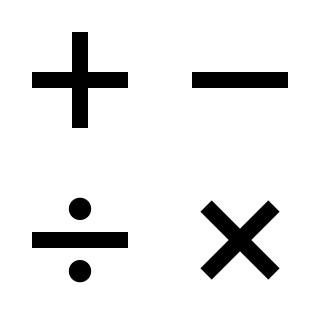
In mathematics, an operation is a calculation from zero or more input values to an output value. The number of operands is the arity of the operation. The most commonly studied operations are binary operations, such as addition and multiplication, and unary operations, such as additive inverse and multiplicative inverse. An operation of arity zero, or nullary operation, is a constant. The mixed product is an example of an operation of arity 3, also called ternary operation. Generally, the arity is supposed to be finite. However, infinitary operations are sometimes considered, in which context the "usual" operations of finite arity are called finitary operations.
An addition-subtraction chain, a generalization of addition chains to include subtraction, is a sequence a0, a1, a2, a3, ... that satisfies
In mathematics, a Bratteli diagram is a combinatorial structure: a graph composed of vertices labelled by positive integers ("level") and unoriented edges between vertices having levels differing by one. The notion was introduced by Ola Bratteli in 1972 in the theory of operator algebras to describe directed sequences of finite-dimensional algebras: it played an important role in Elliott's classification of AF-algebras and the theory of subfactors. Subsequently Anatoly Vershik associated dynamical systems with infinite paths in such graphs.
In mathematics, an algebraic number fieldF is a finite degree field extension of the field of rational numbers Q. Thus F is a field that contains Q and has finite dimension when considered as a vector space over Q.