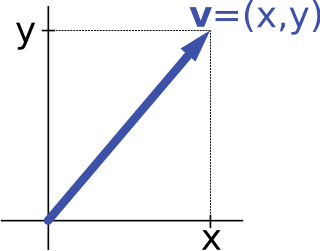In mathematics, a geometric algebra is an extension of elementary algebra to work with geometrical objects such as vectors. Geometric algebra is built out of two fundamental operations, addition and the geometric product. Multiplication of vectors results in higher-dimensional objects called multivectors. Compared to other formalisms for manipulating geometric objects, geometric algebra is noteworthy for supporting vector division and addition of objects of different dimensions.

In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensions is an ordinary sphere, the boundary of a ball in four dimensions is a 3-sphere. A 3-sphere is an example of a 3-manifold and an n-sphere.
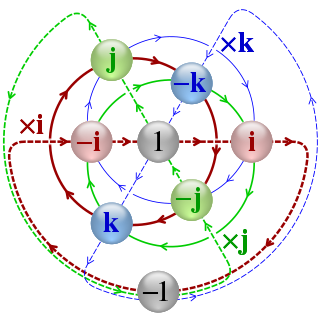
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quaternion as the quotient of two directed lines in a three-dimensional space, or, equivalently, as the quotient of two vectors. Multiplication of quaternions is noncommutative.

In mathematics, a unit vector in a normed vector space is a vector of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in .

Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

Rotation in mathematics is a concept originating in geometry. Any rotation is a motion of a certain space that preserves at least one point. It can describe, for example, the motion of a rigid body around a fixed point. Rotation can have sign : a clockwise rotation is a negative magnitude so a counterclockwise turn has a positive magnitude. A rotation is different from other types of motions: translations, which have no fixed points, and (hyperplane) reflections, each of them having an entire (n − 1)-dimensional flat of fixed points in a n-dimensional space.

In the mathematical field of differential topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle. Technically, Hopf found a many-to-one continuous function from the 3-sphere onto the 2-sphere such that each distinct point of the 2-sphere is mapped from a distinct great circle of the 3-sphere. Thus the 3-sphere is composed of fibers, where each fiber is a circle — one for each point of the 2-sphere.

Alexander Macfarlane FRSE LLD was a Scottish logician, physicist, and mathematician.
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
In abstract algebra, the biquaternions are the numbers w + xi + yj + zk, where w, x, y, and z are complex numbers, or variants thereof, and the elements of {1, i, j, k} multiply as in the quaternion group and commute with their coefficients. There are three types of biquaternions corresponding to complex numbers and the variations thereof:
In abstract algebra, the split-quaternions or coquaternions form an algebraic structure introduced by James Cockle in 1849 under the latter name. They form an associative algebra of dimension four over the real numbers.

In geometry, the orientation, angular position, attitude, bearing, or direction of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it occupies. More specifically, it refers to the imaginary rotation that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement. It may be necessary to add an imaginary translation, called the object's location. The location and orientation together fully describe how the object is placed in space. The above-mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its location does not change when it rotates.
In mathematics, a versor is a quaternion of norm one. The word is derived from Latin versare = "to turn" with the suffix -or forming a noun from the verb. It was introduced by William Rowan Hamilton in the context of his quaternion theory.
A scalar is an element of a field which is used to define a vector space. In linear algebra, real numbers or generally elements of a field are called scalars and relate to vectors in an associated vector space through the operation of scalar multiplication, in which a vector can be multiplied by a scalar in the defined way to produce another vector. Generally speaking, a vector space may be defined by using any field instead of real numbers. Then scalars of that vector space will be elements of the associated field.
In mathematics, a composition algebraA over a field K is a not necessarily associative algebra over K together with a nondegenerate quadratic form N that satisfies
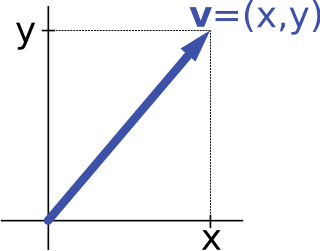
In mathematics and physics, vector notation is a commonly used notation for representing vectors, which may be Euclidean vectors, or more generally, members of a vector space.
William Rowan Hamilton invented quaternions, a mathematical entity in 1843. This article describes Hamilton's original treatment of quaternions, using his notation and terms. Hamilton's treatment is more geometric than the modern approach, which emphasizes quaternions' algebraic properties. Mathematically, quaternions discussed differ from the modern definition only by the terminology which is used.

In mathematics, quaternions are a non-commutative number system that extends the complex numbers. Quaternions and their applications to rotations were first described in print by Olinde Rodrigues in all but name in 1840, but independently discovered by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. They find uses in both theoretical and applied mathematics, in particular for calculations involving three-dimensional rotations.
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts:
In mathematics, a bivector is the vector part of a biquaternion. For biquaternion q = w + xi + yj + zk, w is called the biscalar and xi + yj + zk is its bivector part. The coordinates w, x, y, z are complex numbers with imaginary unit h: