The Game of Life, also known as Conway's Game of Life or simply Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.
A cellular automaton is a discrete model of computation studied in automata theory. Cellular automata are also called cellular spaces, tessellation automata, homogeneous structures, cellular structures, tessellation structures, and iterative arrays. Cellular automata have found application in various areas, including physics, theoretical biology and microstructure modeling.
A tree automaton is a type of state machine. Tree automata deal with tree structures, rather than the strings of more conventional state machines.
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a finite automaton (FA) or finite-state machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
An excitable medium is a nonlinear dynamical system which has the capacity to propagate a wave of some description, and which cannot support the passing of another wave until a certain amount of time has passed.
In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines a relation between sets of strings.
In a cellular automaton, a Garden of Eden is a configuration that has no predecessor. It can be the initial configuration of the automaton but cannot arise in any other way. John Tukey named these configurations after the Garden of Eden in Abrahamic religions, which was created out of nowhere.
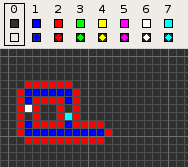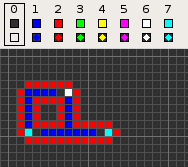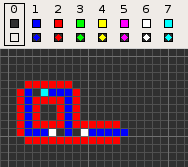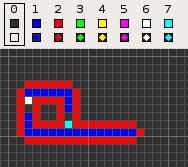
Codd's cellular automaton is a cellular automaton (CA) devised by the British computer scientist Edgar F. Codd in 1968. It was designed to recreate the computation- and construction-universality of von Neumann's CA but with fewer states: 8 instead of 29. Codd showed that it was possible to make a self-reproducing machine in his CA, in a similar way to von Neumann's universal constructor, but never gave a complete implementation.
A block cellular automaton or partitioning cellular automaton is a special kind of cellular automaton in which the lattice of cells is divided into non-overlapping blocks and the transition rule is applied to a whole block at a time rather than a single cell. Block cellular automata are useful for simulations of physical quantities, because it is straightforward to choose transition rules that obey physical constraints such as reversibility and conservation laws.
A cyclic cellular automaton is a kind of cellular automaton rule developed by David Griffeath and studied by several other cellular automaton researchers. In this system, each cell remains unchanged until some neighboring cell has a modular value exactly one unit larger than that of the cell itself, at which point it copies its neighbor's value. One-dimensional cyclic cellular automata can be interpreted as systems of interacting particles, while cyclic cellular automata in higher dimensions exhibit complex spiraling behavior.
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm", which will become the daughter loop. The "genes" instruct it to make three left turns, completing the loop, which then disconnects from its parent.
The firing squad synchronization problem is a problem in computer science and cellular automata in which the goal is to design a cellular automaton that, starting with a single active cell, eventually reaches a state in which all cells are simultaneously active. It was first proposed by John Myhill in 1957 and published in 1962 by Edward F. Moore.
Quantum dot cellular automata are a proposed improvement on conventional computer design (CMOS), which have been devised in analogy to conventional models of cellular automata introduced by John von Neumann.
John von Neumann's universal constructor is a self-replicating machine in a cellular automaton (CA) environment. It was designed in the 1940s, without the use of a computer. The fundamental details of the machine were published in von Neumann's book Theory of Self-Reproducing Automata, completed in 1966 by Arthur W. Burks after von Neumann's death. It is regarded as foundational for automata theory, complex systems, and artificial life. Indeed, Nobel Laureate Sydney Brenner considered Von Neumann's work on self-reproducing automata central to biological theory as well, allowing us to "discipline our thoughts about machines, both natural and artificial."
Cellular automata, as with other multi-agent system models, usually treat time as discrete and state updates as occurring synchronously. The state of every cell in the model is updated together, before any of the new states influence other cells. In contrast, an asynchronous cellular automaton is able to update individual cells independently, in such a way that the new state of a cell affects the calculation of states in neighbouring cells.
A quantum cellular automaton (QCA) is an abstract model of quantum computation, devised in analogy to conventional models of cellular automata introduced by John von Neumann. The same name may also refer to quantum dot cellular automata, which are a proposed physical implementation of "classical" cellular automata by exploiting quantum mechanical phenomena. QCA have attracted a lot of attention as a result of its extremely small feature size and its ultra-low power consumption, making it one candidate for replacing CMOS technology.
Nobili cellular automata (NCA) are a variation of von Neumann cellular automata (vNCA), in which additional states provide means of memory and the interference-free crossing of signal. Nobili cellular automata are the invention of Renato Nobili, a professor of physics at the University of Padova in Padova, Italy. Von Neumann specifically excluded the use of states dedicated to the crossing of signal.
The Byl's loop is an artificial lifeform similar in concept to Langton's loop. It is a two-dimensional, 5-neighbor cellular automaton with 6 states per cell, and was developed in 1989 by John Byl, from the Department of Mathematical Sciences of Trinity Western University.
A reversible cellular automaton is a cellular automaton in which every configuration has a unique predecessor. That is, it is a regular grid of cells, each containing a state drawn from a finite set of states, with a rule for updating all cells simultaneously based on the states of their neighbors, such that the previous state of any cell before an update can be determined uniquely from the updated states of all the cells. The time-reversed dynamics of a reversible cellular automaton can always be described by another cellular automaton rule, possibly on a much larger neighborhood.
