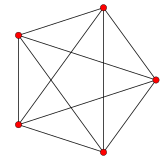
 5-cell |
In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.
 5-cell |
In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.
A4 symmetry, or [3,3,3] is order 120, with Conway quaternion notation +1/60[I×I].21. Its abstract structure is the symmetric group S5. Three forms with symmetric Coxeter diagrams have extended symmetry, [[3,3,3]] of order 240, and Conway notation ±1/60[I×I].2, and abstract structure S5×C2.
Each can be visualized as symmetric orthographic projections in Coxeter planes of the A4 Coxeter group, and other subgroups. Three Coxeter plane 2D projections are given, for the A4, A3, A2 Coxeter groups, showing symmetry order 5,4,3, and doubled on even Ak orders to 10,4,6 for symmetric Coxeter diagrams.
The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.
| # | Name | Coxeter diagram and Schläfli symbols | Coxeter plane graphs | Schlegel diagram | Net | |||
|---|---|---|---|---|---|---|---|---|
| A4 [5] | A3 [4] | A2 [3] | Tetrahedron centered | Dual tetrahedron centered | ||||
| 1 | 5-cell pentachoron | {3,3,3} |  |  |  |  |  | |
| 2 | rectified 5-cell | r{3,3,3} |  | 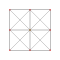 | 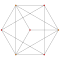 |  |  | |
| 3 | truncated 5-cell | t{3,3,3} |  |  |  |  |  | |
| 4 | cantellated 5-cell | rr{3,3,3} |  | 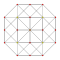 |  |  |  | |
| 7 | cantitruncated 5-cell | tr{3,3,3} |  | 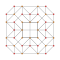 | 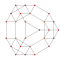 | 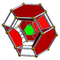 | 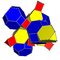 | |
| 8 | runcitruncated 5-cell | t0,1,3{3,3,3} |  |  |  |  |  | |
| # | Name | Coxeter diagram and Schläfli symbols | Coxeter plane graphs | Schlegel diagram | Net | ||
|---|---|---|---|---|---|---|---|
| A4 [[5]] = [10] | A3 [4] | A2 [[3]] = [6] | Tetrahedron centered | ||||
| 5 | *runcinated 5-cell | t0,3{3,3,3} |  | 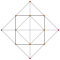 | 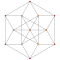 |  |  |
| 6 | *bitruncated 5-cell decachoron | 2t{3,3,3} |  | 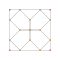 | 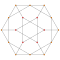 |  |  |
| 9 | *omnitruncated 5-cell | t0,1,2,3{3,3,3} |  | 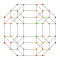 | 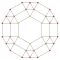 |  | 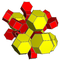 |
The coordinates of uniform 4-polytopes with pentachoric symmetry can be generated as permutations of simple integers in 5-space, all in hyperplanes with normal vector (1,1,1,1,1). The A4 Coxeter group is palindromic, so repeated polytopes exist in pairs of dual configurations. There are 3 symmetric positions, and 6 pairs making the total 15 permutations of one or more rings. All 15 are listed here in order of binary arithmetic for clarity of the coordinate generation from the rings in each corresponding Coxeter diagram.
The number of vertices can be deduced here from the permutations of the number of coordinates, peaking at 5 factorial for the omnitruncated form with 5 unique coordinate values.
| # | Base point | Name (symmetric name) | Coxeter diagram | Vertices | |
|---|---|---|---|---|---|
| 1 | (0, 0, 0, 0, 1) (1, 1, 1, 1, 0) | 5-cell Trirectified 5-cell | 5 | 5!/(4!) | |
| 2 | (0, 0, 0, 1, 1) (1, 1, 1, 0, 0) | Rectified 5-cell Birectified 5-cell | 10 | 5!/(3!2!) | |
| 3 | (0, 0, 0, 1, 2) (2, 2, 2, 1, 0) | Truncated 5-cell Tritruncated 5-cell | 20 | 5!/(3!) | |
| 5 | (0, 1, 1, 1, 2) | Runcinated 5-cell | 20 | 5!/(3!) | |
| 4 | (0, 0, 1, 1, 2) (2, 2, 1, 1, 0) | Cantellated 5-cell Bicantellated 5-cell | 30 | 5!/(2!2!) | |
| 6 | (0, 0, 1, 2, 2) | Bitruncated 5-cell | 30 | 5!/(2!2!) | |
| 7 | (0, 0, 1, 2, 3) (3, 3, 2, 1, 0) | Cantitruncated 5-cell Bicantitruncated 5-cell | 60 | 5!/2! | |
| 8 | (0, 1, 1, 2, 3) (3, 2, 2, 1, 0) | Runcitruncated 5-cell Runcicantellated 5-cell | 60 | 5!/2! | |
| 9 | (0, 1, 2, 3, 4) | Omnitruncated 5-cell | 120 | 5! | |

In geometry, a 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), and cells (polyhedra). Each face is shared by exactly two cells.

In geometry, the 5-cell is a four-dimensional object bounded by 5 tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It is the 4-simplex (Coxeter's polytope), the simplest possible convex regular 4-polytope (four-dimensional analogue of a Platonic solid), and is analogous to the tetrahedron in three dimensions and the triangle in two dimensions. The pentachoron is a four dimensional pyramid with a tetrahedral base.

In geometry, the 120-cell is the convex regular 4-polytope with Schläfli symbol {5,3,3}. It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hecatonicosachoron, dodecacontachoron and hecatonicosahedroid.

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In four-dimensional geometry, a runcinated 5-cell is a convex uniform 4-polytope, being a runcination of the regular 5-cell.

In four-dimensional geometry, a cantellated tesseract is a convex uniform 4-polytope, being a cantellation of the regular tesseract.
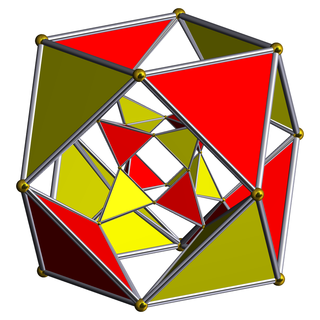
In geometry, the rectified tesseract, rectified 8-cell is a uniform 4-polytope bounded by 24 cells: 8 cuboctahedra, and 16 tetrahedra. It has half the vertices of a runcinated tesseract, with its construction, called a runcic tesseract.

In four-dimensional geometry, a cantellated 5-cell is a convex uniform 4-polytope, being a cantellation of the regular 5-cell.

In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In six-dimensional geometry, a pentellated 6-simplex is a convex uniform 6-polytope with 5th order truncations of the regular 6-simplex.
In five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation (runcination) of the regular 5-orthoplex.
In four-dimensional Euclidean geometry, the rectified tesseractic honeycomb is a uniform space-filling tessellation in Euclidean 4-space. It is constructed by a rectification of a tesseractic honeycomb which creates new vertices on the middle of all the original edges, rectifying the cells into rectified tesseracts, and adding new 16-cell facets at the original vertices. Its vertex figure is an octahedral prism, {3,4}×{}.
In four-dimensional Euclidean geometry, the cantellated tesseractic honeycomb is a uniform space-filling tessellation in Euclidean 4-space. It is constructed by a cantellation of a tesseractic honeycomb creating cantellated tesseracts, and new 24-cell and octahedral prism facets at the original vertices.

In 4-dimensional geometry, there are 15 uniform 4-polytopes with B4 symmetry. There are two regular forms, the tesseract, and 16-cell with 16 and 8 vertices respectively.

In 4-dimensional geometry, there are 15 uniform polytopes with H4 symmetry. Two of these, the 120-cell and 600-cell, are regular.
In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D4 symmetry, all are shared with higher symmetry constructions in the B4 or F4 symmetry families. there is also one half symmetry alternation, the snub 24-cell.