Kinematics is a branch of classical mechanics that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that caused the motion. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum.
In mathematics, matrix multiplication or matrix product is a binary operation that produces a matrix from two matrices with entries in a field, or, more generally, in a ring or even a semiring. The matrix product is designed for representing the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. In more detail, if A is an n × m matrix and B is an m × p matrix, their matrix product AB is an n × p matrix, in which the m entries across a row of A are multiplied with the m entries down a column of B and summed to produce an entry of AB. When two linear maps are represented by matrices, then the matrix product represents the composition of the two maps.
In linear algebra, Cramer's rule is an explicit formula for the solution of a system of linear equations with as many equations as unknowns, valid whenever the system has a unique solution. It expresses the solution in terms of the determinants of the (square) coefficient matrix and of matrices obtained from it by replacing one column by the column vector of right-hand-sides of the equations. It is named after Gabriel Cramer (1704–1752), who published the rule for an arbitrary number of unknowns in 1750, although Colin Maclaurin also published special cases of the rule in 1748.
In the mathematical field of differential geometry, a metric tensor is a type of function which takes as input a pair of tangent vectors v and w at a point of a surface and produces a real number scalar g(v, w) in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean space. In the same way as a dot product, metric tensors are used to define the length of and angle between tangent vectors. Through integration, the metric tensor allows one to define and compute the length of curves on the manifold.
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants".
In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned.
Differential geometry of curves is the branch of geometry that deals with smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus.
In control engineering, a state-space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations or difference equations. State variables are variables whose values evolve through time in a way that depends on the values they have at any given time and also depends on the externally imposed values of input variables. Output variables’ values depend on the values of the state variables.
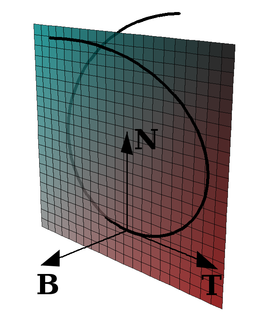
In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a continuous, differentiable curve in three-dimensional Euclidean space ℝ3, or the geometric properties of the curve itself irrespective of any motion. More specifically, the formulas describe the derivatives of the so-called tangent, normal, and binormal unit vectors in terms of each other. The formulas are named after the two French mathematicians who independently discovered them: Jean Frédéric Frenet, in his thesis of 1847, and Joseph Alfred Serret in 1851. Vector notation and linear algebra currently used to write these formulas were not yet in use at the time of their discovery.
Quantum statistical mechanics is statistical mechanics applied to quantum mechanical systems. In quantum mechanics a statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be shown under various mathematical formalisms for quantum mechanics. One such formalism is provided by quantum logic.
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices. It collects the various partial derivatives of a single function with respect to many variables, and/or of a multivariate function with respect to a single variable, into vectors and matrices that can be treated as single entities. This greatly simplifies operations such as finding the maximum or minimum of a multivariate function and solving systems of differential equations. The notation used here is commonly used in statistics and engineering, while the tensor index notation is preferred in physics.

In mathematics, the Weierstrass–Enneper parameterization of minimal surfaces is a classical piece of differential geometry.
In the elementary differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the plane of curvature. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas.
A parametric surface is a surface in the Euclidean space which is defined by a parametric equation with two parameters Parametric representation is a very general way to specify a surface, as well as implicit representation. Surfaces that occur in two of the main theorems of vector calculus, Stokes' theorem and the divergence theorem, are frequently given in a parametric form. The curvature and arc length of curves on the surface, surface area, differential geometric invariants such as the first and second fundamental forms, Gaussian, mean, and principal curvatures can all be computed from a given parametrization.

In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet–Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves. In the geometry of surfaces, the geodesic torsion describes how a surface twists about a curve on the surface. The companion notion of curvature measures how moving frames "roll" along a curve "without twisting".
In geometry, the polar sine generalizes the sine function of angle to the vertex angle of a polytope. It is denoted by psin.
In analytical mechanics, the mass matrix is a symmetric matrix M that expresses the connection between the time derivative of the generalized coordinate vector q of a system and the kinetic energy T of that system, by the equation