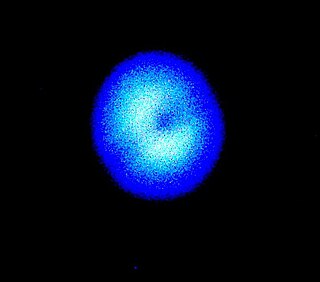
Diffraction refers to various phenomena that occur when a wave encounters an obstacle or a slit. It is defined as the bending of waves around the corners of an obstacle or aperture into the region of geometrical shadow of the obstacle. In classical physics, the diffraction phenomenon is described as the interference of waves according to the Huygens–Fresnel principle that treats each point in the wave-front as a collection of individual spherical wavelets. These characteristic behaviors are exhibited when a wave encounters an obstacle or a slit that is comparable in size to its wavelength. Similar effects occur when a light wave travels through a medium with a varying refractive index, or when a sound wave travels through a medium with varying acoustic impedance. Diffraction has an impact on the acoustic space. Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-rays and radio waves.

A Fresnel zone, named after physicist Augustin-Jean Fresnel, is one of a series of confocal prolate ellipsoidal regions of space between and around a transmitting antenna and a receiving antenna system. The regions are used to understand and compute the strength of waves propagating between a transmitter and a receiver, as well as predict whether obstructions near the line joining the transmitter and receiver will cause significant interference.
Path loss, or path attenuation, is the reduction in power density (attenuation) of an electromagnetic wave as it propagates through space. Path loss is a major component in the analysis and design of the link budget of a telecommunication system.
Angular resolution or spatial resolution describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object, thereby making it a major determinant of image resolution. In physics and geosciences, the term spatial resolution refers to the precision of a measurement with respect to space.

The near field and far field are regions of the electromagnetic field (EM) around an object, such as a transmitting antenna, or the result of radiation scattering off an object. Non-radiative 'near-field' behaviours of electromagnetic fields dominate close to the antenna or scattering object, while electromagnetic radiation 'far-field' behaviours dominate at greater distances.

In optics, the Airy disk and Airy pattern are descriptions of the best-focused spot of light that a perfect lens with a circular aperture can make, limited by the diffraction of light. The Airy disk is of importance in physics, optics, and astronomy.

A zone plate is a device used to focus light or other things exhibiting wave character. Unlike lenses or curved mirrors however, zone plates use diffraction instead of refraction or reflection. Based on analysis by Augustin-Jean Fresnel, they are sometimes called Fresnel zone plates in his honor. The zone plate's focusing ability is an extension of the Arago spot phenomenon caused by diffraction from an opaque disc.

The Friis transmission formula is used in telecommunications engineering, equating the power at the terminals of a receive antenna as the product of power density of the incident wave and the effective aperture of the receiving antenna under idealized conditions given another antenna some distance away transmitting a known amount of power. The formula was presented first by Danish-American radio engineer Harald T. Friis in 1946. The formula is sometimes referenced as the Friis transmission equation.
The Strehl ratio is a measure of the quality of optical image formation, originally proposed by Karl Strehl, after whom the term is named. Used variously in situations where optical resolution is compromised due to lens aberrations or due to imaging through the turbulent atmosphere, the Strehl ratio has a value between 0 and 1, with a hypothetical, perfectly unaberrated optical system having a Strehl ratio of 1.
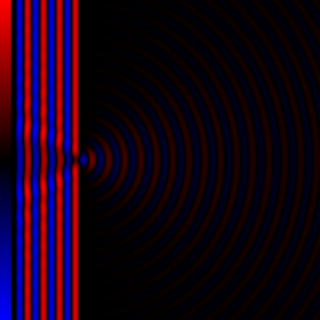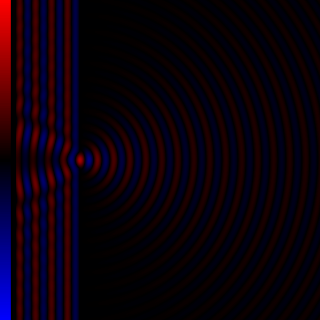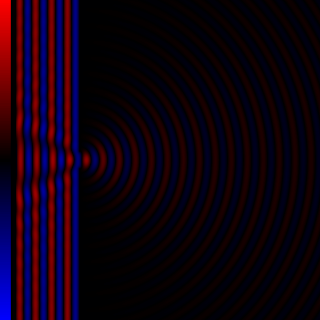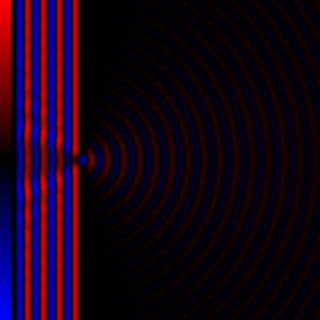
Diffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations.

The Talbot effect is a near-field diffraction effect first observed in 1836 by Henry Fox Talbot. When a plane wave is incident upon a periodic diffraction grating, the image of the grating is repeated at regular distances away from the grating plane. The regular distance is called the Talbot length, and the repeated images are called self images or Talbot images. Furthermore, at half the Talbot length, a self-image also occurs, but phase-shifted by half a period. At smaller regular fractions of the Talbot length, sub-images can also be observed. At one quarter of the Talbot length, the self-image is halved in size, and appears with half the period of the grating. At one eighth of the Talbot length, the period and size of the images is halved again, and so forth creating a fractal pattern of sub images with ever-decreasing size, often referred to as a Talbot carpet.
Focus recovery from a defocused image is an ill-posed problem since it loses the component of high frequency. Most of the methods for focus recovery are based on depth estimation theory. The Linear canonical transform (LCT) gives a scalable kernel to fit many well-known optical effects. Using LCTs to approximate an optical system for imaging and inverting this system, theoretically permits recovery of a defocused image.
Rayleigh distance in optics is the axial distance from a radiating aperture to a point at which the path difference between the axial ray and an edge ray is λ / 4.
An approximation of the Rayleigh Distance is
, in which Z is the Rayleigh distance, D is the aperture of radiation, λ the wavelength.
This approximation can be derived as follows. Consider a right angled triangle with sides adjacent
, opposite
and hypotenuse
. According to Pythagorean theorem,
Kirchhoff's diffraction formula
can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen. The equation is derived by making several approximations to the Kirchhoff integral theorem which uses Green's theorem to derive the solution to the homogeneous wave equation.
Fresnel zone antennas are reflector antennas that focus the signal by using the phase shifting property of the antenna surface, rather than its shape. There are three type of Fresnel zone antennas, namely, Fresnel zone plate, offset Fresnel zone plate antennas and phase correcting reflective array or "Reflectarray" antennas. They are a class of diffractive antennas and have been used from radio frequencies to X rays.
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens.