
A finite-state machine (FSM) or finite-state automaton, finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of states at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a transition. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types—deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed.
In theoretical computer science and formal language theory, a regular language is a formal language that can be defined by a regular expression, in the strict sense in theoretical computer science.

Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
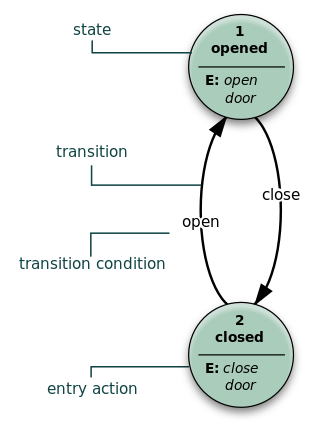
A state diagram is a type of diagram used in computer science and related fields to describe the behavior of systems. State diagrams require that the system described is composed of a finite number of states; sometimes, this is indeed the case, while at other times this is a reasonable abstraction. Many forms of state diagrams exist, which differ slightly and have different semantics.
In the theory of computation, a Mealy machine is a finite-state machine whose output values are determined both by its current state and the current inputs. This is in contrast to a Moore machine, whose output values are determined solely by its current state. A Mealy machine is a deterministic finite-state transducer: for each state and input, at most one transition is possible.
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science. The computability of a problem is closely linked to the existence of an algorithm to solve the problem.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In computer science, the process calculi are a diverse family of related approaches for formally modelling concurrent systems. Process calculi provide a tool for the high-level description of interactions, communications, and synchronizations between a collection of independent agents or processes. They also provide algebraic laws that allow process descriptions to be manipulated and analyzed, and permit formal reasoning about equivalences between processes. Leading examples of process calculi include CSP, CCS, ACP, and LOTOS. More recent additions to the family include the π-calculus, the ambient calculus, PEPA, the fusion calculus and the join-calculus.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines relations between sets of strings.
In mathematics, a Markov decision process (MDP) is a discrete-time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying optimization problems solved via dynamic programming. MDPs were known at least as early as the 1950s; a core body of research on Markov decision processes resulted from Ronald Howard's 1960 book, Dynamic Programming and Markov Processes. They are used in many disciplines, including robotics, automatic control, economics and manufacturing. The name of MDPs comes from the Russian mathematician Andrey Markov as they are an extension of Markov chains.
A learning automaton is one type of machine learning algorithm studied since 1970s. Learning automata select their current action based on past experiences from the environment. It will fall into the range of reinforcement learning if the environment is stochastic and a Markov decision process (MDP) is used.
Automata-based programming is a programming paradigm in which the program or part of it is thought of as a model of a finite-state machine (FSM) or any other formal automaton. Sometimes a potentially infinite set of possible states is introduced, and such a set can have a complicated structure, not just an enumeration.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.
In mathematics and theoretical computer science, an automatic sequence (also called a k-automatic sequence or a k-recognizable sequence when one wants to indicate that the base of the numerals used is k) is an infinite sequence of terms characterized by a finite automaton. The n-th term of an automatic sequence a(n) is a mapping of the final state reached in a finite automaton accepting the digits of the number n in some fixed base k.
Automata-based programming is a programming technology. Its defining characteristic is the use of finite state machines to describe program behavior. The transition graphs of state machines are used in all stages of software development. Automata-based programming technology was introduced by Anatoly Shalyto in 1991. Switch-technology was developed to support automata-based programming. Automata-based programming is considered to be rather general purpose program development methodology than just another one finite state machine implementation.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
In automata theory, a branch of theoretical computer science, an ω-automaton is a variation of finite automata that runs on infinite, rather than finite, strings as input. Since ω-automata do not stop, they have a variety of acceptance conditions rather than simply a set of accepting states.
In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata.
In computational learning theory, induction of regular languages refers to the task of learning a formal description of a regular language from a given set of example strings. Although E. Mark Gold has shown that not every regular language can be learned this way, approaches have been investigated for a variety of subclasses. They are sketched in this article. For learning of more general grammars, see Grammar induction.






