
In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:
In geometry, a polygon is a plane figure made up of line segments connected to form a closed polygonal chain.

A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are coprime (that is, they have no common divisor larger than 1). For example, (3, 4, 5) is a primitive Pythagorean triple whereas (6, 8, 10) is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle.
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients arising in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although other mathematicians studied it centuries before him in Persia, India, China, Germany, and Italy.
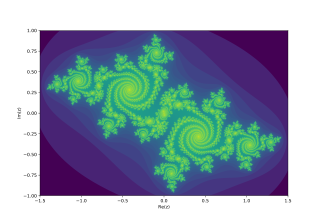
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.

In mathematics, a root of unity, occasionally called a de Moivre number, is any complex number that yields 1 when raised to some positive integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform.
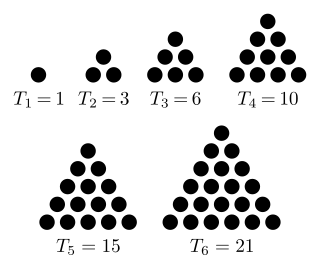
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The nth triangular number is the number of dots in the triangular arrangement with n dots on each side, and is equal to the sum of the n natural numbers from 1 to n. The sequence of triangular numbers, starting with the 0th triangular number, is

In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles Catalan.

In geometry, the problem of dividing a circle into areas by means of an inscribed polygon with n sides in such a way as to maximise the number of areas created by the edges and diagonals, sometimes called Moser's circle problem, has a solution by an inductive method. The greatest possible number of regions, rG = , giving the sequence 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, .... Though the first five terms match the geometric progression 2n − 1, it deviates at n = 6, showing the risk of generalising from only a few observations.

In mathematics and combinatorics, a centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice. The following figures illustrate this arrangement for the first four centered hexagonal numbers:
The On-Line Encyclopedia of Integer Sequences (OEIS) is an online database of integer sequences. It was created and maintained by Neil Sloane while researching at AT&T Labs. He transferred the intellectual property and hosting of the OEIS to the OEIS Foundation in 2009. Sloane is the chairman of the OEIS Foundation.

A cone is a three-dimensional geometric shape that tapers smoothly from a flat base to a point called the apex or vertex.

In geometry, an arrangement of lines is the subdivision of the plane formed by a collection of lines. Problems of counting the features of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.
154 is the natural number following 153 and preceding 155.

In mathematics, the cake number, denoted by Cn, is the maximum of the number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake. It is the 3D analogue of the lazy caterer's sequence.
277 is the natural number following 276 and preceding 278.
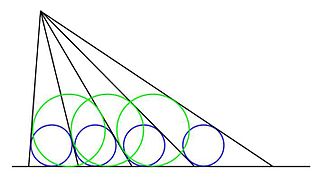
In geometry, the equal incircles theorem derives from a Japanese Sangaku, and pertains to the following construction: a series of rays are drawn from a given point to a given line such that the inscribed circles of the triangles formed by adjacent rays and the base line are equal. In the illustration the equal blue circles define the spacing between the rays, as described.

Bernoulli's triangle is an array of partial sums of the binomial coefficients. For any non-negative integer n and for any integer k included between 0 and n, the component in row n and column k is given by:
301 is the natural number following 300 and preceding 302.























