 24-cell |
In 4-dimensional geometry, there are 9 uniform 4-polytopes with F4 symmetry, and one chiral half symmetry, the snub 24-cell. There is one self-dual regular form, the 24-cell with 24 vertices.
 24-cell |
In 4-dimensional geometry, there are 9 uniform 4-polytopes with F4 symmetry, and one chiral half symmetry, the snub 24-cell. There is one self-dual regular form, the 24-cell with 24 vertices.
Each can be visualized as symmetric orthographic projections in Coxeter planes of the F4 Coxeter group, and other subgroups.
The 3D picture are drawn as Schlegel diagram projections, centered on the cell at pos. 3, with a consistent orientation, and the 5 cells at position 0 are shown solid.
| # | Name Coxeter diagram Schläfli symbol | Graph | Schlegel diagram | Net | |||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12] | B4 [8] | B3 [6] | B2 [4] | Octahedron centered | Dual octahedron centered | ||||
| 1 | 24-cell (rectified 16-cell) {3,4,3} = r{3,3,4} |  |  | 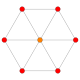 |  | 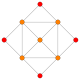 |  |  | |
| 2 | rectified 24-cell (cantellated 16-cell) r{3,4,3} = rr{3,3,4} |  |  |  |  |  |  |  | |
| 3 | truncated 24-cell (cantitruncated 16-cell) t{3,4,3} = tr{3,3,4} |  |  |  |  |  |  | 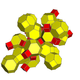 | |
| 4 | cantellated 24-cell rr{3,4,3} |  |  |  | 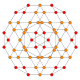 |  |  |  | |
| 5 | cantitruncated 24-cell tr{3,4,3} |  |  |  |  |  |  |  | |
| 6 | runcitruncated 24-cell t0,1,3{3,4,3} |  |  | 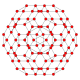 | 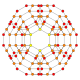 | 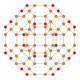 |  |  | |
| # | Name Coxeter diagram Schläfli symbol | Graph | Schlegel diagram | Net | |||
|---|---|---|---|---|---|---|---|
| F4 [[12]] = [24] | B4 [8] | B3 [6] | B2 [[4]] = [8] | Octahedron centered | |||
| 7 | *runcinated 24-cell t0,3{3,4,3} |  |  |  | 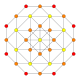 |  |  |
| 8 | *bitruncated 24-cell 2t{3,4,3} |  |  |  |  |  |  |
| 9 | *omnitruncated 24-cell t0,1,2,3{3,4,3} |  |  |  |  |  |  |
| # | Name Coxeter diagram Schläfli symbol | Graph | Schlegel diagram | Orthogonal Projection | Net | ||||
|---|---|---|---|---|---|---|---|---|---|
| F4 [12]+ | B4 [8] | B3 [6]+ | B2 [4] | Octahedron centered | Dual octahedron centered | Octahedron centered | |||
| 10 | snub 24-cell s{3,4,3} |  |  | 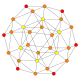 |  |  |  | 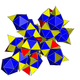 | |
| 11 Nonuniform | runcic snub 24-cell s3{3,4,3} |  |  |  |  | ||||
Vertex coordinates for all 15 forms are given below, including dual configurations from the two regular 24-cells. (The dual configurations are named in bold.) Active rings in the first and second nodes generate points in the first column. Active rings in the third and fourth nodes generate the points in the second column. The sum of each of these points are then permutated by coordinate positions, and sign combinations. This generates all vertex coordinates. Edge lengths are 2.
The only exception is the snub 24-cell, which is generated by half of the coordinate permutations, only an even number of coordinate swaps. φ=(√5+1)/2.
| # | Base point(s) t(0,1) | Base point(s) t(2,3) | Schläfli symbol | Name | Coxeter diagram |
|---|---|---|---|---|---|
| 1 | (0,0,1,1)√2 | {3,4,3} | 24-cell | ||
| 2 | (0,1,1,2)√2 | r{3,4,3} | rectified 24-cell | ||
| 3 | (0,1,2,3)√2 | t{3,4,3} | truncated 24-cell | ||
| 10 | (0,1,φ,φ+1)√2 | s{3,4,3} | snub 24-cell | ||
| 2 | (0,2,2,2) (1,1,1,3) | r{3,4,3} | rectified 24-cell | ||
| 4 | (0,2,2,2) + (1,1,1,3) + | (0,0,1,1)√2 " | rr{3,4,3} | cantellated 24-cell | |
| 8 | (0,2,2,2) + (1,1,1,3) + | (0,1,1,2)√2 " | 2t{3,4,3} | bitruncated 24-cell | |
| 5 | (0,2,2,2) + (1,1,1,3) + | (0,1,2,3)√2 " | tr{3,4,3} | cantitruncated 24-cell | |
| 1 | (0,0,0,2) (1,1,1,1) | {3,4,3} | 24-cell | ||
| 7 | (0,0,0,2) + (1,1,1,1) + | (0,0,1,1)√2 " | t0,3{3,4,3} | runcinated 24-cell | |
| 4 | (0,0,0,2) + (1,1,1,1) + | (0,1,1,2)√2 " | t1,3{3,4,3} | cantellated 24-cell | |
| 6 | (0,0,0,2) + (1,1,1,1) + | (0,1,2,3)√2 " | t0,1,3{3,4,3} | runcitruncated 24-cell | |
| 3 | (1,1,1,5) (1,3,3,3) (2,2,2,4) | t{3,4,3} | truncated 24-cell | ||
| 6 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,0,1,1)√2 " " | t0,2,3{3,4,3} | runcitruncated 24-cell | |
| 5 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,1,1,2)√2 " " | tr{3,4,3} | cantitruncated 24-cell | |
| 9 | (1,1,1,5) + (1,3,3,3) + (2,2,2,4) + | (0,1,2,3)√2 " " | t0,1,2,3{3,4,3} | Omnitruncated 24-cell | |

In geometry, a uniform 4-polytope is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedra, and faces are regular polygons.

In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.

In geometry, a truncated 24-cell is a uniform 4-polytope formed as the truncation of the regular 24-cell.
In geometry, a truncated tesseract is a uniform 4-polytope formed as the truncation of the regular tesseract.

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

In geometry, a rectified 120-cell is a uniform 4-polytope formed as the rectification of the regular 120-cell.

In four-dimensional geometry, a cantellated 24-cell is a convex uniform 4-polytope, being a cantellation of the regular 24-cell.

In four-dimensional geometry, a runcinated 24-cell is a convex uniform 4-polytope, being a runcination of the regular 24-cell.

In geometry, a truncated 120-cell is a uniform 4-polytope formed as the truncation of the regular 120-cell.

In four-dimensional geometry, a cantellated 120-cell is a convex uniform 4-polytope, being a cantellation of the regular 120-cell.

In four-dimensional geometry, a runcinated 120-cell is a convex uniform 4-polytope, being a runcination of the regular 120-cell.

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.

In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope facets.
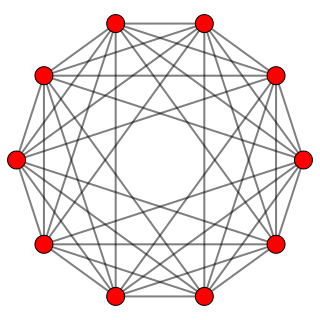
In five-dimensional geometry, a runcinated 5-orthoplex is a convex uniform 5-polytope with 3rd order truncation (runcination) of the regular 5-orthoplex.
In four-dimensional Euclidean geometry, the snub 24-cell honeycomb, or snub icositetrachoric honeycomb is a uniform space-filling tessellation by snub 24-cells, 16-cells, and 5-cells. It was discovered by Thorold Gosset with his 1900 paper of semiregular polytopes. It is not semiregular by Gosset's definition of regular facets, but all of its cells (ridges) are regular, either tetrahedra or icosahedra.

In 4-dimensional geometry, there are 9 uniform polytopes with A4 symmetry. There is one self-dual regular form, the 5-cell with 5 vertices.

In 4-dimensional geometry, there are 15 uniform 4-polytopes with B4 symmetry. There are two regular forms, the tesseract and 16-cell, with 16 and 8 vertices respectively.

In 4-dimensional geometry, there are 15 uniform polytopes with H4 symmetry. Two of these, the 120-cell and 600-cell, are regular.
In 4-dimensional geometry, there are 7 uniform 4-polytopes with reflections of D4 symmetry, all are shared with higher symmetry constructions in the B4 or F4 symmetry families. there is also one half symmetry alternation, the snub 24-cell.