 |
In probability theory, Proebsting's paradox is an argument that appears to show that the Kelly criterion can lead to ruin. Although it can be resolved mathematically, it raises some interesting issues about the practical application of Kelly, especially in investing. It was named and first discussed by Edward O. Thorp in 2008. [1] The paradox was named for Todd Proebsting, its creator.
If a bet is equally likely to win or lose, and pays b times the stake for a win, the Kelly bet is:
times wealth. [2] For example, if a 50/50 bet pays 2 to 1, Kelly says to bet 25% of wealth. If a 50/50 bet pays 5 to 1, Kelly says to bet 40% of wealth.
Now suppose a gambler is offered 2 to 1 payout and bets 25%. What should he do if the payout on new bets changes to 5 to 1? He should choose f* to maximize:
because if he wins he will have 1.5 (the 0.5 from winning the 25% bet at 2 to 1 odds) plus 5f*; and if he loses he must pay 0.25 from the first bet, and f* from the second. Taking the derivative with respect to f* and setting it to zero gives:
which can be rewritten:
So f* = 0.225.
The paradox is that the total bet, 0.25 + 0.225 = 0.475, is larger than the 0.4 Kelly bet if the 5 to 1 odds are offered from the beginning. It is counterintuitive that you bet more when some of the bet is at unfavorable odds. Todd Proebsting emailed Ed Thorp asking about this.
Ed Thorp realized the idea could be extended to give the Kelly bettor a nonzero probability of being ruined. He showed that if a gambler is offered 2 to 1 odds, then 4 to 1, then 8 to 1 and so on (2n to 1 for n = 1 to infinity) Kelly says to bet:
each time. The sum of all these bets is 1. So a Kelly gambler has a 50% chance of losing his entire wealth.
In general, if a bettor makes the Kelly bet on a 50/50 proposition with a payout of b1, and then is offered b2, he will bet a total of:
The first term is what the bettor would bet if offered b2 initially. The second term is positive if f2 > f1, meaning that if the payout improves, the Kelly bettor will bet more than he would if just offered the second payout, while if the payout gets worse he will bet less than he would if offered only the second payout.
Many bets have the feature that payoffs and probabilities can change before the outcome is determined. In sports betting for example, the line may change several times before the event is held, and news may come out (such as an injury or weather forecast) that changes the probability of an outcome. In investing, a stock originally bought at $20 per share might be available now at $10 or $30 or any other price. Some sports bettors try to make income from anticipating line changes rather than predicting event outcomes. Some traders concentrate on possible short-term price movements of a security rather than its long-term fundamental prospects. [3]
A classic investing example is a trader who has exposure limits, say he is not allowed to have more than $1 million at risk in any one stock. That doesn't mean he cannot lose more than $1 million. If he buys $1 million of the stock at $20 and it goes to $10, he can buy another $500,000. If it then goes to $5, he can buy another $500,000. If it goes to zero, he can lose an infinite amount of money, despite never having more than $1 million at risk. [4]
There is no paradox. Kelly's criterion is to maximise expected rate of growth; only under restricted conditions does it correspond to maximising the log. One easy way to dismiss the paradox is to note that Kelly assumes that probabilities do not change.
A Kelly bettor who knows odds might change could factor this into a more complex Kelly bet. For example suppose a Kelly bettor is given a one-time opportunity to bet a 50/50 proposition at odds of 2 to 1. He knows there is a 50% chance that a second one-time opportunity will be offered at 5 to 1. Now he should maximize:
with respect to both f1 and f2. The answer turns out to be bet zero at 2 to 1, and wait for the chance of betting at 5 to 1, in which case you bet 40% of wealth. If the probability of being offered 5 to 1 odds is less than 50%, some amount between zero and 25% will be bet at 2 to 1. If the probability of being offered 5 to 1 odds is more than 50%, the Kelly bettor will actually make a negative bet at 2 to 1 odds (that is, bet on the 50/50 outcome with payout of 1/2 if he wins and paying 1 if he loses). In either case, his bet at 5 to 1 odds, if the opportunity is offered, is 40% minus 0.7 times his 2 to 1 bet.
What the paradox says, essentially, is that if a Kelly bettor has incorrect beliefs about what future bets may be offered, he can make suboptimal choices, and even go broke. The Kelly criterion is supposed to do better than any essentially different strategy in the long run and have zero chance of ruin, as long as the bettor knows the probabilities and payouts. [2]
More light on the issues was shed by an independent consideration of the problem by Aaron Brown, also communicated to Ed Thorp by email. In this formulation, the assumption is the bettor first sells back the initial bet, then makes a new bet at the second payout. In this case his total bet is:
which looks very similar to the formula above for the Proebsting formulation, except that the sign is reversed on the second term and it is multiplied by an additional term.
For example, given the original example of a 2 to 1 payout followed by a 5 to 1 payout, in this formulation the bettor first bets 25% of wealth at 2 to 1. When the 5 to 1 payout is offered, the bettor can sell back the original bet for a loss of 0.125. His 2 to 1 bet pays 0.5 if he wins and costs 0.25 if he loses. At the new 5 to 1 payout, he could get a bet that pays 0.625 if he wins and costs 0.125 if he loses, this is 0.125 better than his original bet in both states. Therefore his original bet now has a value of -0.125. Given his new wealth level of 0.875, his 40% bet (the Kelly amount for the 5 to 1 payout) is 0.35.
The two formulations are equivalent. In the original formulation, the bettor has 0.25 bet at 2 to 1 and 0.225 bet at 5 to 1. If he wins, he gets 2.625 and if he loses he has 0.525. In the second formulation, the bettor has 0.875 and 0.35 bet at 5 to 1. If he wins, he gets 2.625 and if he loses he has 0.525.
The second formulation makes clear that the change in behavior results from the mark-to-market loss the investor experiences when the new payout is offered. This is a natural way to think in finance, less natural to a gambler. In this interpretation, the infinite series of doubling payouts does not ruin the Kelly bettor by enticing him to overbet, it extracts all his wealth through changes beyond his control.
In probability theory, the expected value is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would "expect" to get in reality.
Roulette is a casino game which was likely developed from the Italian game Biribi. In the game, a player may choose to place a bet on a single number, various groupings of numbers, the color red or black, whether the number is odd or even, or if the numbers are high (19–36) or low (1–18).
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value of log45 ≈ 1.16 precisely reflect it. Empirical observation has shown that this 80-20 distribution fits a wide range of cases, including natural phenomena and human activities.
Fixed-odds betting is a form of gambling where individuals place bets on the outcome of an event, such as sports matches or horse races, at predetermined odds. In fixed-odds betting, the odds are fixed and determined at the time of placing the bet. These odds reflect the likelihood of a particular outcome occurring. If the bettor's prediction is correct, they receive a payout based on the fixed odds. This means that the potential winnings are known at the time of placing the bet, regardless of any changes in the odds leading up to the event.
In probability theory, odds provide a measure of the likelihood of a particular outcome. They are calculated as the ratio of the number of events that produce that outcome to the number that do not. Odds are commonly used in gambling and statistics.
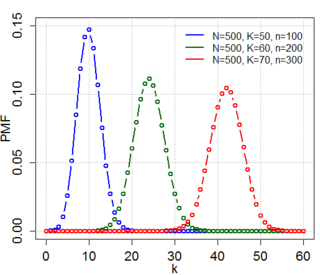
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.
In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression is estimating the parameters of a logistic model. Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.
A martingale is a class of betting strategies that originated from and were popular in 18th-century France. The simplest of these strategies was designed for a game in which the gambler wins the stake if a coin comes up heads and loses if it comes up tails. The strategy had the gambler double the bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. Thus the strategy is an instantiation of the St. Petersburg paradox.
In a thought experiment proposed by the Italian probabilist Bruno de Finetti in order to justify Bayesian probability, an array of wagers is coherent precisely if it does not expose the wagerer to certain loss regardless of the outcomes of events on which they are wagering, even if their opponent makes the most judicious choices.
In statistics, gambler's ruin is the fact that a gambler playing a game with negative expected value will eventually go broke, regardless of their betting system.
The St. Petersburg paradox or St. Petersburg lottery is a paradox involving the game of flipping a coin where the expected payoff of the theoretical lottery game approaches infinity but nevertheless seems to be worth only a very small amount to the participants. The St. Petersburg paradox is a situation where a naïve decision criterion that takes only the expected value into account predicts a course of action that presumably no actual person would be willing to take. Several resolutions to the paradox have been proposed, including the impossible amount of money a casino would need to continue the game indefinitely.
Vigorish is the fee charged by a bookmaker for accepting a gambler's wager. In American English, it can also refer to the interest owed a loanshark in consideration for credit. The term came to English usage via Yiddish slang, which was itself a loanword from Russian.
Fan-Tan, or fantan is a gambling game long played in China. It is a game of pure chance.
Edward Oakley Thorp is an American mathematics professor, author, hedge fund manager, and blackjack researcher. He pioneered the modern applications of probability theory, including the harnessing of very small correlations for reliable financial gain.
The two envelopes problem, also known as the exchange paradox, is a paradox in probability theory. It is of special interest in decision theory and for the Bayesian interpretation of probability theory. It is a variant of an older problem known as the necktie paradox. The problem is typically introduced by formulating a hypothetical challenge like the following example:
Imagine you are given two identical envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?
The Boy or Girl paradox surrounds a set of questions in probability theory, which are also known as The Two Child Problem, Mr. Smith's Children and the Mrs. Smith Problem. The initial formulation of the question dates back to at least 1959, when Martin Gardner featured it in his October 1959 "Mathematical Games column" in Scientific American. He titled it The Two Children Problem, and phrased the paradox as follows:
In probability theory, the Kelly criterion is a formula for sizing a bet. The Kelly bet size is found by maximizing the expected value of the logarithm of wealth, which is equivalent to maximizing the expected geometric growth rate. Assuming that the expected returns are known, the Kelly criterion leads to higher wealth than any other strategy in the long run. J. L. Kelly Jr, a researcher at Bell Labs, described the criterion in 1956.
Asian handicap betting is a form of betting on football in which teams are handicapped according to their form so that a stronger team must win by more goals for a bet on them to win. The system originated in Indonesia and gained popularity in the early 21st century. It is a form of spread betting. Handicaps typically range from one-quarter goal to several goals, in increments of half- or even quarter-goals.
In gambling, Dutching is sharing the risk of losing across a number of runners by backing more than one selection in a race or event. One needs to calculate the correct stake to place on each selection so that the return is the same if any of them wins. Although not foolproof, because handicapping is still involved, there have been successful bettors throughout history who have applied this system. This is not to be confused with what constitutes a Dutch book which is when a bookmaker goes overbroke.
The mathematics of gambling is a collection of probability applications encountered in games of chance and can get included in game theory. From a mathematical point of view, the games of chance are experiments generating various types of aleatory events, and it is possible to calculate by using the properties of probability on a finite space of possibilities.
