In mathematics, one can often define a direct product of objects already known, giving a new one. This induces a structure on the Cartesian product of the underlying sets from that of the contributing objects. More abstractly, one talks about the product in category theory, which formalizes these notions.

In mathematics, when the elements of some set have a notion of equivalence, then one may naturally split the set into equivalence classes. These equivalence classes are constructed so that elements and belong to the same equivalence class if, and only if, they are equivalent.
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".

In mathematics, especially order theory, a partial order on a set is an arrangement such that, for certain pairs of elements, one precedes the other. The word partial is used to indicate that not every pair of elements needs to be comparable; that is, there may be pairs for which neither element precedes the other. Partial orders thus generalize total orders, in which every pair is comparable.

In mathematics, topological groups are the combination of groups and topological spaces, i.e. they are groups and topological spaces at the same time, such that the continuity condition for the group operations connects these two structures together and consequently they are not independent from each other.

In mathematics, rings are algebraic structures that generalize fields: multiplication need not be commutative and multiplicative inverses need not exist. Informally, a ring is a set equipped with two binary operations satisfying properties analogous to those of addition and multiplication of integers. Ring elements may be numbers such as integers or complex numbers, but they may also be non-numerical objects such as polynomials, square matrices, functions, and power series.
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula. As formulas are entirely constituted with symbols of various types, many symbols are needed for expressing all mathematics.
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions. Many important categories have obvious interpretations as concrete categories, for example the category of topological spaces and the category of groups, and trivially also the category of sets itself. On the other hand, the homotopy category of topological spaces is not concretizable, i.e. it does not admit a faithful functor to the category of sets.

In mathematics, a direct limit is a way to construct a object from many objects that are put together in a specific way. These objects may be groups, rings, vector spaces or in general objects from any category. The way they are put together is specified by a system of homomorphisms between those smaller objects. The direct limit of the objects , where ranges over some directed set , is denoted by .

In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology.
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by enumerating its elements, or stating the properties that its members must satisfy.
In mathematics, a sheaf is a tool for systematically tracking data attached to the open sets of a topological space and defined locally with regard to them. For example, for each open set, the data could be the ring of continuous functions defined on that open set. Such data are well behaved in that they can be restricted to smaller open sets, and also the data assigned to an open set are equivalent to all collections of compatible data assigned to collections of smaller open sets covering the original open set.
In mathematics, K-theory is, roughly speaking, the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is a cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It is also a fundamental tool in the field of operator algebras. It can be seen as the study of certain kinds of invariants of large matrices.
In mathematics, a function space is a set of functions between two fixed sets. Often, the domain and/or codomain will have additional structure which is inherited by the function space. For example, the set of functions from any set X into a vector space has a natural vector space structure given by pointwise addition and scalar multiplication. In other scenarios, the function space might inherit a topological or metric structure, hence the name function space.

In mathematics, Pontryagin duality is a duality between locally compact abelian groups that allows generalizing Fourier transform to all such groups, which include the circle group, the finite abelian groups, and the additive group of the integers, the real numbers, and every finite-dimensional vector space over the reals or a p-adic field.
In algebraic geometry, motives is a theory proposed by Alexander Grothendieck in the 1960s to unify the vast array of similarly behaved cohomology theories such as singular cohomology, de Rham cohomology, etale cohomology, and crystalline cohomology. Philosophically, a "motif" is the "cohomology essence" of a variety.
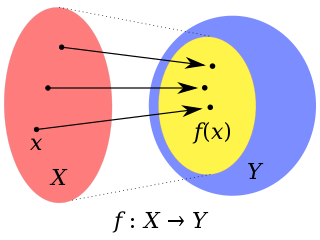
In mathematics, the image of a function is the set of all output values it may produce.
In mathematics, the Grothendieck group, or group of differences, of a commutative monoid M is a certain abelian group. This abelian group is constructed from M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
This is a glossary of algebraic geometry.






























