In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type. The word homomorphism comes from the Ancient Greek language: ὁμός meaning "same" and μορφή meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German ähnlich meaning "similar" to ὁμός meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925).
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation .
In category theory, an epimorphism is a morphism f : X → Y that is right-cancellative in the sense that, for all objects Z and all morphisms g1, g2: Y → Z,
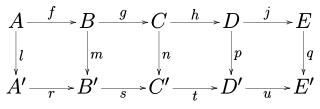
In mathematics, and especially in category theory, a commutative diagram is a diagram such that all directed paths in the diagram with the same start and endpoints lead to the same result. It is said that commutative diagrams play the role in category theory that equations play in algebra.

Homological algebra is the branch of mathematics that studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and David Hilbert.
In mathematics, specifically category theory, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and arrows.
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.
In mathematics, the derived categoryD(A) of an abelian category A is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on A. The construction proceeds on the basis that the objects of D(A) should be chain complexes in A, with two such chain complexes considered isomorphic when there is a chain map that induces an isomorphism on the level of homology of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hypercohomology. The definitions lead to a significant simplification of formulas otherwise described by complicated spectral sequences.
In universal algebra, a variety of algebras or equational class is the class of all algebraic structures of a given signature satisfying a given set of identities. For example, the groups form a variety of algebras, as do the abelian groups, the rings, the monoids etc. According to Birkhoff's theorem, a class of algebraic structures of the same signature is a variety if and only if it is closed under the taking of homomorphic images, subalgebras and (direct) products. In the context of category theory, a variety of algebras, together with its homomorphisms, forms a category; these are usually called finitary algebraic categories.
This is a glossary of properties and concepts in category theory in mathematics.
In category theory, a strict 2-category is a category with "morphisms between morphisms", that is, where each hom-set itself carries the structure of a category. It can be formally defined as a category enriched over Cat.
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms ('arrows') called 'weak equivalences', 'fibrations' and 'cofibrations' satisfying certain axioms relating them. These abstract from the category of topological spaces or of chain complexes. The concept was introduced by Daniel G. Quillen (1967).
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.
In model theory, a branch of mathematical logic, the Hrushovski construction generalizes the Fraïssé limit by working with a notion of strong substructure rather than . It can be thought of as a kind of "model-theoretic forcing", where a (usually) stable structure is created, called the generic or rich model. The specifics of determine various properties of the generic, with its geometric properties being of particular interest. It was initially used by Ehud Hrushovski to generate a stable structure with an "exotic" geometry, thereby refuting Zil'ber's Conjecture.
This is a glossary of algebraic geometry.
In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples.
In mathematics, structural Ramsey theory is a categorical generalisation of Ramsey theory, rooted in the idea that many important results of Ramsey theory have "similar" logical structure. The key observation is noting that these Ramsey-type theorems can be expressed as the assertion that a certain category has the Ramsey property.
In mathematical logic, specifically in the discipline of model theory, the Fraïssé limit is a method used to construct (infinite) mathematical structures from their (finite) substructures. It is a special example of the more general concept of a direct limit in a category. The technique was developed in the 1950s by its namesake, French logician Roland Fraïssé.








