
In geometry, an apeirotope or infinite polytope is a generalized polytope which has infinitely many facets.

In geometry, an apeirotope or infinite polytope is a generalized polytope which has infinitely many facets.
An abstract n-polytope is a partially ordered set P (whose elements are called faces) such that P contains a least face and a greatest face, each maximal totally ordered subset (called a flag) contains exactly n + 2 faces, P is strongly connected, and there are exactly two faces that lie strictly between a and b are two faces whose ranks differ by two. [1] [2] An abstract polytope is called an abstract apeirotope if it has infinitely many faces. [3]
An abstract polytope is called regular if its automorphism group Γ(P) acts transitively on all of the flags of P. [4]
There are two main geometric classes of apeirotope: [5]
In general, a honeycomb in n dimensions is an infinite example of a polytope in n + 1 dimensions.
Tilings of the plane and close-packed space-fillings of polyhedra are examples of honeycombs in two and three dimensions respectively.
A line divided into infinitely many finite segments is an example of an apeirogon.
A skew apeirogon in two dimensions forms a zig-zag line in the plane. If the zig-zag is even and symmetrical, then the apeirogon is regular.
Skew apeirogons can be constructed in any number of dimensions. In three dimensions, a regular skew apeirogon traces out a helical spiral and may be either left- or right-handed.
There are three regular skew apeirohedra, which look rather like polyhedral sponges:
There are thirty regular apeirohedra in Euclidean space. [6] These include those listed above, as well as (in the plane) polytopes of type: {∞,3}, {∞,4}, {∞,6} and in 3-dimensional space, blends of these with either an apeirogon or a line segment, and the "pure" 3-dimensional apeirohedra (12 in number)

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.

In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. Such dual figures remain combinatorial or abstract polyhedra, but not all can also be constructed as geometric polyhedra. Starting with any given polyhedron, the dual of its dual is the original polyhedron.
In elementary geometry, a polytope is a geometric object with flat sides (faces). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions n as an n-dimensional polytope or n-polytope. For example, a two-dimensional polygon is a 2-polytope and a three-dimensional polyhedron is a 3-polytope. In this context, "flat sides" means that the sides of a (k + 1)-polytope consist of k-polytopes that may have (k – 1)-polytopes in common.
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different equivalent definitions are used; a common one is that the faces are congruent regular polygons which are assembled in the same way around each vertex.

In geometry, the Schläfli symbol is a notation of the form that defines regular polytopes and tessellations.

In mathematics, a regular polytope is a polytope whose symmetry group acts transitively on its flags, thus giving it the highest degree of symmetry. In particular, all its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are themselves regular polytopes of dimension j≤ n.
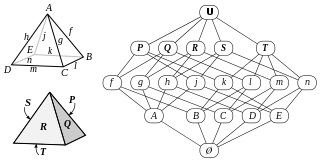
In mathematics, an abstract polytope is an algebraic partially ordered set which captures the dyadic property of a traditional polytope without specifying purely geometric properties such as points and lines.

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive. It follows that all vertices are congruent.

In geometry, a truncated 5-cell is a uniform 4-polytope formed as the truncation of the regular 5-cell.

In geometry, an apeirogon or infinite polygon is a polygon with an infinite number of sides. Apeirogons are the rank 2 case of infinite polytopes. In some literature, the term "apeirogon" may refer only to the regular apeirogon, with an infinite dihedral group of symmetries.

In geometry, a skew polygon is a polygon whose vertices are not all coplanar. Skew polygons must have at least four vertices. The interior surface of such a polygon is not uniquely defined.

In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons.
In geometry, a complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one.
In geometry, a skew apeirohedron is an infinite skew polyhedron consisting of nonplanar faces or nonplanar vertex figures, allowing the figure to extend indefinitely without folding round to form a closed surface.

In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon in which every n – 1 consecutive sides belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a regular polyhedron is a skew polygon such that every two consecutive sides belongs to one of the faces. Petrie polygons are named for mathematician John Flinders Petrie.

In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedra which include the possibility of nonplanar faces or vertex figures. Coxeter looked at skew vertex figures which created new 4-dimensional regular polyhedra, and much later Branko Grünbaum looked at regular skew faces.
In geometry, an infinite skew polygon or skew apeirogon is an infinite 2-polytope with vertices that are not all colinear. Infinite zig-zag skew polygons are 2-dimensional infinite skew polygons with vertices alternating between two parallel lines. Infinite helical polygons are 3-dimensional infinite skew polygons with vertices on the surface of a cylinder.

In geometry, a regular skew apeirohedron is an infinite regular skew polyhedron. They have either skew regular faces or skew regular vertex figures.