
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.

A hyperbolic spiral is a plane curve, which can be described in polar coordinates by the equation

In mathematics, a semicircle is a one-dimensional locus of points that forms half of a circle. The full arc of a semicircle always measures 180°. It has only one line of symmetry. In non-technical usage, the term "semicircle" is sometimes used to refer to a half-disk, which is a two-dimensional geometric shape that also includes the diameter segment from one end of the arc to the other as well as all the interior points.

In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line that contains their diameters.
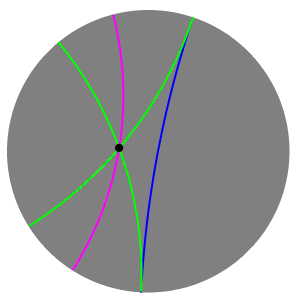
In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel.

In geometry, the area enclosed by a circle of radius r is πr2. Here the Greek letter π represents the constant ratio of the circumference of any circle to its diameter, approximately equal to 3.14159.

In hyperbolic geometry an ideal triangle is a hyperbolic triangle whose three vertices all are ideal points. Ideal triangles are also sometimes called triply asymptotic triangles or trebly asymptotic triangles. The vertices are sometimes called ideal vertices. All ideal triangles are congruent.
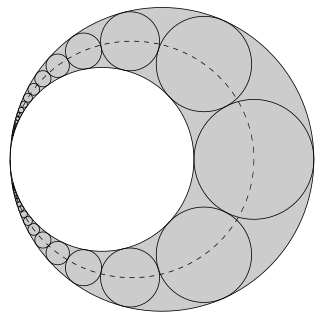
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.

In geometry, the Bankoff circle or Bankoff triplet circle is a certain Archimedean circle that can be constructed from an arbelos; an Archimedean circle is any circle with area equal to each of Archimedes' twin circles. The Bankoff circle was first constructed by Leon Bankoff in 1974.

In geometry, the twin circles are two special circles associated with an arbelos. An arbelos is determined by three collinear points A, B, and C, and is the curvilinear triangular region between the three semicircles that have AB, BC, and AC as their diameters. If the arbelos is partitioned into two smaller regions by a line segment through the middle point of A, B, and C, perpendicular to line ABC, then each of the two twin circles lies within one of these two regions, tangent to its two semicircular sides and to the splitting segment.

In geometry, the Schoch line is a line defined from an arbelos and named by Peter Woo after Thomas Schoch, who had studied it in conjunction with the Schoch circles.

In geometry, Archimedes' quadruplets are four congruent circles associated with an arbelos. Introduced by Frank Power in the summer of 1998, each have the same area as Archimedes' twin circles, making them Archimedean circles.

The salinon is a geometrical figure that consists of four semicircles. It was first introduced in the Book of Lemmas, a work attributed to Archimedes.

In geometry, the Woo circles, introduced by Peter Y. Woo, are a set of infinitely many Archimedean circles.

The Book of Lemmas is a book attributed to Archimedes by Thābit ibn Qurra, though the authorship of the book is questionable. It consists of fifteen propositions (lemmas) on circles.

In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles, where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual closed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.
In geometry, the Schoch circles are twelve Archimedean circles constructed by Thomas Schoch.
In geometry, tangent circles are circles in a common plane that intersect in a single point. There are two types of tangency: internal and external. Many problems and constructions in geometry are related to tangent circles; such problems often have real-life applications such as trilateration and maximizing the use of materials.

























