
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space Cn. The existence of a complex derivative in a neighbourhood is a very strong condition: it implies that a holomorphic function is infinitely differentiable and locally equal to its own Taylor series (analytic). Holomorphic functions are the central objects of study in complex analysis.

In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane. Essentially, it says that if is holomorphic in a simply connected domain Ω, then for any simply closed contour in Ω, that contour integral is zero.
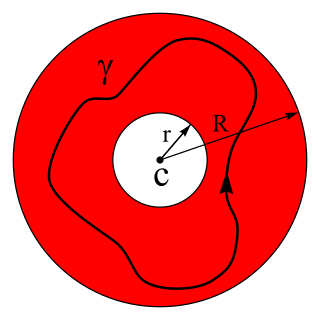
In mathematics, the Laurent series of a complex function is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.

In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all derivatives of a holomorphic function. Cauchy's formula shows that, in complex analysis, "differentiation is equivalent to integration": complex differentiation, like integration, behaves well under uniform limits – a result that does not hold in real analysis.

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities. Residues can be computed quite easily and, once known, allow the determination of general contour integrals via the residue theorem.

In complex analysis, the residue theorem, sometimes called Cauchy's residue theorem, is a powerful tool to evaluate line integrals of analytic functions over closed curves; it can often be used to compute real integrals and infinite series as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula. The residue theorem should not be confused with special cases of the generalized Stokes' theorem; however, the latter can be used as an ingredient of its proof.

In mathematics, the winding number or winding index of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point, i.e., the curve's number of turns. For certain open plane curves, the number of turns may be non-integer. The winding number depends on the orientation of the curve, and it is negative if the curve travels around the point clockwise.

In vector calculus, Green's theorem relates a line integral around a simple closed curve C to a double integral over the plane region D bounded by C. It is the two-dimensional special case of Stokes' theorem.
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function for which there exists a positive number such that for all is constant. Equivalently, non-constant holomorphic functions on have unbounded images.

In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic.

In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.

Rouché's theorem, named after Eugène Rouché, states that for any two complex-valued functions f and g holomorphic inside some region with closed contour , if |g(z)| < |f(z)| on , then f and f + g have the same number of zeros inside , where each zero is counted as many times as its multiplicity. This theorem assumes that the contour is simple, that is, without self-intersections. Rouché's theorem is an easy consequence of a stronger symmetric Rouché's theorem described below.
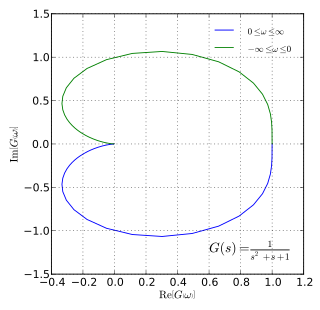
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer Felix Strecker at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a dynamical system.
In mathematics, the Borel–Carathéodory theorem in complex analysis shows that an analytic function may be bounded by its real part. It is an application of the maximum modulus principle. It is named for Émile Borel and Constantin Carathéodory.
In mathematics, holomorphic functional calculus is functional calculus with holomorphic functions. That is to say, given a holomorphic function f of a complex argument z and an operator T, the aim is to construct an operator, f(T), which naturally extends the function f from complex argument to operator argument. More precisely, the functional calculus defines a continuous algebra homomorphism from the holomorphic functions on a neighbourhood of the spectrum of T to the bounded operators.
In mathematics, the Nørlund–Rice integral, sometimes called Rice's method, relates the nth forward difference of a function to a line integral on the complex plane. It commonly appears in the theory of finite differences and has also been applied in computer science and graph theory to estimate binary tree lengths. It is named in honour of Niels Erik Nørlund and Stephen O. Rice. Nørlund's contribution was to define the integral; Rice's contribution was to demonstrate its utility by applying saddle-point techniques to its evaluation.
In complex analysis, Jordan's lemma is a result frequently used in conjunction with the residue theorem to evaluate contour integrals and improper integrals. The lemma is named after the French mathematician Camille Jordan.

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral is used as well, although that is typically reserved for line integrals in the complex plane.
In probability theory and directional statistics, a wrapped probability distribution is a continuous probability distribution that describes data points that lie on a unit n-sphere. In one dimension, a wrapped distribution consists of points on the unit circle. If is a random variate in the interval with probability density function (PDF) , then is a circular variable distributed according to the wrapped distribution and is an angular variable in the interval distributed according to the wrapped distribution .
In thermal quantum field theory, the Matsubara frequency summation is the summation over discrete imaginary frequencies. It takes the following form
![The simple contour C (black), the zeros of f (blue) and the poles of f (red). Here we have
1
2
p
i
[?]
C
f
'
(
z
)
f
(
z
)
d
z
=
4
-
5.
{\displaystyle {\frac {1}{2\pi i}}\oint _{C}{f'(z) \over f(z)}\,dz=4-5.\,} Argument principle1.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/2/25/Argument_principle1.svg/212px-Argument_principle1.svg.png)






















