Azimuthal equidistant projection

Last updated May 15, 2024

The azimuthal equidistant projection is an azimuthal map projection. It has the useful properties that all points on the map are at proportionally correct distances from the center point, and that all points on the map are at the correct azimuth (direction) from the center point. A useful application for this type of projection is a polar projection which shows all meridians (lines of longitude) as straight, with distances from the pole represented correctly.

The flag of the United Nations contains an example of a polar azimuthal equidistant projection. The polar azimuthal equidistant projection has also been adopted by 21st century Flat Earthers as a map of the Flat Earth, particularly due to its use in the UN flag and its depiction of Antarctica as a ring around the edge of the Earth.

History

While it may have been used by ancient Egyptians for star maps in some holy books,^[1] the earliest text describing the azimuthal equidistant projection is an 11th-century work by al-Biruni.^[2]

An example of this system is the world map by ‛Ali b. Ahmad al-Sharafi of Sfax in 1571.^[3]

The projection appears in many Renaissance maps, and Gerardus Mercator used it for an inset of the north polar regions in sheet 13 and legend 6 of his well-known 1569 map. In France and Russia this projection is named "Postel projection" after Guillaume Postel, who used it for a map in 1581.^[4] Many modern star chart planispheres use the polar azimuthal equidistant projection.

Comparison of the Azimuthal equidistant projection and some azimuthal projections centred on 90° N at the same scale, ordered by projection altitude in Earth radii. (click for detail)

The polar azimuthal equidistant projection has also been adopted by 21st century Flat Earthers as a map of the Flat Earth, particularly due to its use in the UN flag and its depiction of Antarctica as a ring around the edge of the Earth.^[5]

Mathematical definition

A point on the globe is chosen as "the center" in the sense that mapped distances and azimuth directions from that point to any other point will be correct. That point, (φ₀, λ₀), will project to the center of a circular projection, with φ referring to latitude and λ referring to longitude. All points along a given azimuth will project along a straight line from the center, and the angle θ that the line subtends from the vertical is the azimuth angle. The distance from the center point to another projected point ρ is the arc length along a great circle between them on the globe. By this description, then, the point on the plane specified by (θ,ρ) will be projected to Cartesian coordinates:

x=\rho \sin \theta ,\qquad y=-\rho \cos \theta

The relationship between the coordinates (θ,ρ) of the point on the globe, and its latitude and longitude coordinates (φ, λ) is given by the equations: ^[6]

{\begin{aligned}\cos {\frac {\rho }{R}}&=\sin \varphi _{0}\sin \varphi +\cos \varphi _{0}\cos \varphi \cos \left(\lambda -\lambda _{0}\right)\\\tan \theta &={\frac {\cos \varphi \sin \left(\lambda -\lambda _{0}\right)}{\cos \varphi _{0}\sin \varphi -\sin \varphi _{0}\cos \varphi \cos \left(\lambda -\lambda _{0}\right)}}\end{aligned}}

When the center point is the north pole, φ₀ equals $\pi /2$ and λ₀ is arbitrary, so it is most convenient to assign it the value of 0. This assignment significantly simplifies the equations for ρ_u and θ to:

\rho =R\left({\frac {\pi }{2}}-\varphi \right),\qquad \theta =\lambda ~~

Limitation

With the circumference of the Earth being approximately 40,000 km (24,855 mi), the maximum distance that can be displayed on an azimuthal equidistant projection map is half the circumference, or about 20,000 km (12,427 mi). For distances less than 10,000 km (6,214 mi) distortions are minimal. For distances 10,000–15,000 km (6,214–9,321 mi) the distortions are moderate. Distances greater than 15,000 km (9,321 mi) are severely distorted.

If the azimuthal equidistant projection map is centered about a point whose antipodal point lies on land and the map is extended to the maximum distance of 20,000 km (12,427 mi) the antipode point smears into a large circle. This is shown in the example of two maps centered about Los Angeles, and Taipei. The antipode for Los Angeles is in the south Indian Ocean hence there is not much significant distortion of land masses for the Los Angeles centered map except for East Africa and Madagascar. On the other hand, Taipei's antipode is near the Argentina–Paraguay border, causing the Taipei centered map to severely distort South America.

Sample azimuthal equidistant projection maps

Map centered about Los Angeles, whose antipodal point is in the south Indian Ocean

California

Map centered about Taipei, whose antipodal point is near the Argentina–Paraguay border

Taiwan
Brazil
Paraguay
Argentina
Chile
Bolivia
Uruguay

Red circles: 10,000 km radius circles

Purple circles: 15,000 km radius circles

Applications

An azimuthal equidistant projection centered on Sydney Gcmsyd.jpg — An azimuthal equidistant projection centered on Sydney

Azimuthal equidistant projection maps can be useful in terrestrial point to point communication. This type of projection allows the operator to easily determine in which direction to point their directional antenna. The operator simply finds on the map the location of the target transmitter or receiver (i.e. the other antenna being communicated with) and uses the map to determine the azimuth angle needed to point the operator's antenna. The operator would use an electric rotator to point the antenna. The map can also be used in one way communication. For example if the operator is looking to receive signals from a distant radio station, this type of projection could help identify the direction of the distant radio station. In order for the map to be useful, the map should be centered as close as possible about the location of the operator's antenna.^{[ citation needed ]}

Azimuthal equidistant projection maps can also be useful to show ranges of ballistic missiles, as demonstrated by the map centered on North Korea showing the country's missile range.

Related Research Articles

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three numbers, : the radial distance of the radial liner connecting the point to the fixed point of origin ; the polar angle θ of the radial line r; and the azimuthal angle φ of the radial line r.

In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as

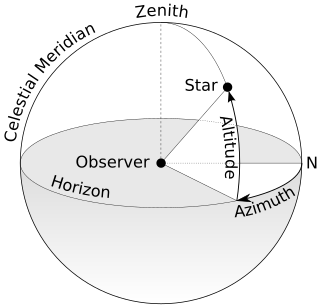
An azimuth is the angular measurement in a spherical coordinate system which represents the horizontal angle from a cardinal direction, most commonly north.

<span class="mw-page-title-main">Ellipsoid</span> Quadric surface that looks like a deformed sphere

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.

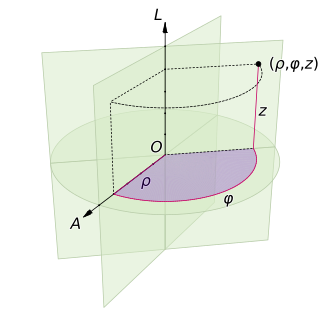
A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis (axis L in the image opposite), the direction from the axis relative to a chosen reference direction (axis A), and the distance from a chosen reference plane perpendicular to the axis (plane containing the purple section). The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

Orthographic projection in cartography has been used since antiquity. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic projection is at infinite distance. It depicts a hemisphere of the globe as it appears from outer space, where the horizon is a great circle. The shapes and areas are distorted, particularly near the edges.

The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.

In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.

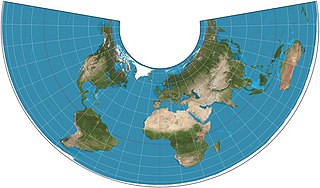
The Albers equal-area conic projection, or Albers projection, is a conic, equal area map projection that uses two standard parallels. Although scale and shape are not preserved, distortion is minimal between the standard parallels.

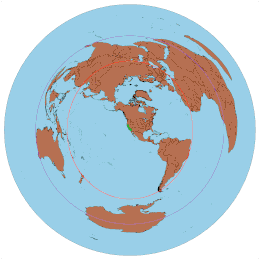
The Lambert azimuthal equal-area projection is a particular mapping from a sphere to a disk. It accurately represents area in all regions of the sphere, but it does not accurately represent angles. It is named for the Swiss mathematician Johann Heinrich Lambert, who announced it in 1772. "Zenithal" being synonymous with "azimuthal", the projection is also known as the Lambert zenithal equal-area projection.

<span class="mw-page-title-main">Great-circle navigation</span> Flight or sailing route along the shortest path between two points on a globes surface

Great-circle navigation or orthodromic navigation is the practice of navigating a vessel along a great circle. Such routes yield the shortest distance between two points on the globe.

Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as $. Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential.$

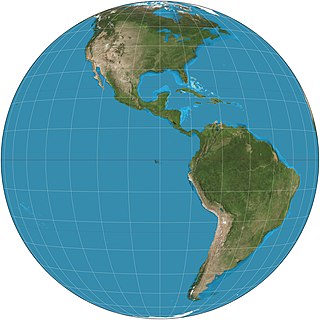
The General Perspective projection is a map projection. When the Earth is photographed from space, the camera records the view as a perspective projection. When the camera is aimed toward the center of the Earth, the resulting projection is called Vertical Perspective. When aimed in other directions, the resulting projection is called a Tilted Perspective.

In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.

In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.

In mathematics, log-polar coordinates is a coordinate system in two dimensions, where a point is identified by two numbers, one for the logarithm of the distance to a certain point, and one for an angle. Log-polar coordinates are closely connected to polar coordinates, which are usually used to describe domains in the plane with some sort of rotational symmetry. In areas like harmonic and complex analysis, the log-polar coordinates are more canonical than polar coordinates.

The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west.

Side-looking airborne radar (SLAR) is an aircraft- or satellite-mounted imaging radar pointing perpendicular to the direction of flight. A squinted (nonperpendicular) mode is also possible. SLAR can be fitted with a standard antenna or an antenna using synthetic aperture.

The Hammer retroazimuthal projection is a modified azimuthal proposed by Ernst Hermann Heinrich Hammer in 1910. As a retroazimuthal projection, azimuths (directions) are correct from any point to the designated center point. Additionally, all distances from the center of the map are proportional to what they are on the globe. In whole-world presentation, the back and front hemispheres overlap, making the projection a non-injective function. The back hemisphere can be rotated 180° to avoid overlap, but in this case, any azimuths measured from the back hemisphere must be corrected.

In cartography, an equivalent, authalic, or equal-area projection is a map projection that preserves relative area measure between any and all map regions. Equivalent projections are widely used for thematic maps showing scenario distribution such as population, farmland distribution, forested areas, and so forth, because an equal-area map does not change apparent density of the phenomenon being mapped.

References

↑ SNYDER, John P. (1997). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 0-226-76747-7., p.29
↑ David A. KING (1996), "Astronomy and Islamic society: Qibla, gnomics and timekeeping", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science , Vol. 1, p. 128–184 [153]. Routledge, London and New York.
↑ Edward S. Kennedy, 1996, Mathematical geography, in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science , Vol. 1, Routledge, London and New York.
↑ Snyder 1997, p. 29
↑ "Fact Check: The UN Flag Does NOT Show Flat Earth | Lead Stories". leadstories.com. 2022-09-12. Retrieved 2024-02-04.
↑ Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 228. ISBN 978-0160033681. Archived from the original on 2010-07-01. Retrieved 2018-03-29.

External links

Table of examples and properties of all common projections, from radicalcartography.net
Online Azimuthal Equidistant Map Generator
An interactive Java Applet to study the metric deformations of the Azimuthal Equidistant Projection.
GeographicLib provides a class for performing azimuthal equidistant projections centered at any point on the ellipsoid.
Animated US National Weather Service Wind Data for Azimuthal equidistant projection.
Generate an Azimuthal equidistant projection from any point on Earth from ns6t.net.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[Snyder-1] SNYDER, John P. (1997). Flattening the earth: two thousand years of map projections. University of Chicago Press. ISBN 0-226-76747-7., p.29

[2] David A. KING (1996), "Astronomy and Islamic society: Qibla, gnomics and timekeeping", in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science , Vol. 1, p. 128–184 [153]. Routledge, London and New York.

[3] Edward S. Kennedy, 1996, Mathematical geography, in Roshdi Rashed, ed., Encyclopedia of the History of Arabic Science , Vol. 1, Routledge, London and New York.

[4] Snyder 1997, p. 29

[5] "Fact Check: The UN Flag Does NOT Show Flat Earth | Lead Stories". leadstories.com. 2022-09-12. Retrieved 2024-02-04.

[Album-6] Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 228. ISBN 978-0160033681. Archived from the original on 2010-07-01. Retrieved 2018-03-29.

[1]

[2]

[3]

[4]

[5]

[6]